x^x³ = 3

Here's a problem. Let $f(x) = x^{x^3}$. Obviously, $f(1) = 1$ and $f$ grows with $x$ without bound. It follows that the equation

$x^{x^3} = 3$

has a solution greater than $1.$ Find at least one such solution.

We are only concerned with positive $x.$ Introduce $y = x^3,$ then $x^{y} = 3.$ Take the logarithm of both sides of both equations:

$ \begin{align} \mbox{ln}(y) &= 3\cdot \mbox{ln}(x) \\ y\cdot \mbox{ln}(x) &= \mbox{ln}(3), \end{align} $

which simplifies to

$y\cdot \mbox{ln}(y) = 3\cdot \mbox{ln}(3).$

The latter equation is trivially solved by $y = 3.$ (We may observe in passing that the equation has no other real solutions. Indeed, the function $g(y) = y\cdot \mbox{ln}(y)$ is negative for $y \lt 1$ and, since it's derivative $g'(y) = \mbox{ln}(y) + 1$ is positive, is increasing for $y \gt 1$.)

Therefore, $3 = x^3$, and $x = 3^{1/3}.$

Well, we got one solution to the equation $x^{x^3} = 3$ and may consider the problem solved and the case closed. However, I was quite surprised to arrive at that solution. For, note that the value $x = 3^{1/3}$ solves, by definition, another equation, namely $x^{3} = 3.$ The situations begs for a generalization. $x = 3^{1/3}$ solves

$x^{3} = 3,$ and
$x^{x^{3}} = 3.$

Will it also solve $x^{x^{x^{3}}} = 3$? Yes, of course. Since $3 = x^{3}$ and $x^{x^{3}} = 3$ we can replace in the latter the exponent $3$ with $x^{3},$ which then asserts that indeed $x^{x^{x^{3}}} = 3.$

Having made the first step, why not to continue? We can substitute $x^{3}$ for the exponent $3$ in the new equation, to obtain $x^{x^{x^{x^{3}}}} = 3$.

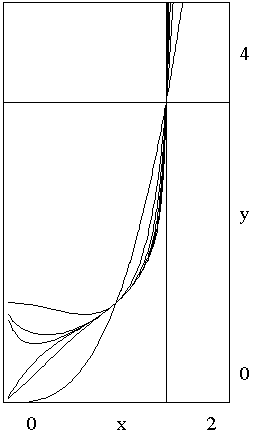
Let's define

$\displaystyle f_{n}(x) = x^{x^{\space\ldots ^{x^{3}}}}.$

with n occurrences of $x,$ so that $f_{1}(x) = x^{3}$ and $f_{2}(x) = x^{x^{3}}.$ Then, by an obvious induction, $f_{n}(3^{1/3}) = 3.$ On the right, you can see the graphs of the first few functions $f_{n}.$

The next logical step is to replace $3$ with an arbitrary parameter $a.$ For positive $a,$ define

$f_{n}(x, a) = x^{x^{\space\ldots ^{x^{a}}}}$

with $n$ $x$'s and consider the equation $f_{n}(x, a) = a.$ Had we started with say $x^{x^{x^{a}}} = a$, would have it been immediately obvious that the equation has a solution $x = a^{1/a}?$

We see that, for all $n,$ $f_{n}(a^{1/a}, a) = a.$ But that's not all. We may also consider an equation with an "infinite" exponent: $x^{x^{x^{\ldots}}} = a.$ If the expression $x^{x^{x^{\ldots}}}$ does at all have any sense, the equation will again imply $x^{a} = a,$ so that this equation, too, has the same solution $a^{1/a}.$ But how can we define such an infinite exponent? The answer is, in a standard way we should check whether the sequence

$s_{1} = x, s_{2} = x^{x}, s_{3} = x^{x^{x}}, \ldots$

has a limit. If it does, the infinite exponent $x^{x^{x^{\ldots}}}$ is declared to equal this limit. For $1 \lt x \lt e^{1/e}$ the limit in fact exists (see the note at the bottom of the page), and this is how we prove that.

The sequence $\{s_{n}\}$ is monotone increasing and is bounded from above. (It's a well known fact that bounded monotone sequences have a limit.) Indeed, since $x \gt 1,$ $s_{1} \gt 1.$ We then also have

$s_{2} = x^{s_{1}} \gt x^{1} = s_{1}$

and, more generally, by induction,

$s_{n+1} = x^{s_{n}} \gt x^{s_{n-1}} = s_{n}.$

The sequence $\{s_{n}\}$ is also bounded from above. To see that, first of all observe that if

(1)

$x^{y} = y$

then $x$ and $y$ are either both greater or both less than $1.$ If they are greater than 1 then $x \lt y.$ This starts an induction: $s_{1} \lt y.$ Assume $s_{n} \lt y.$ Then

$s_{n+1} = x^{s_{n}} \lt x^{y} = y.$

We conclude that sequence $\{s_{n}\}$ has a limit, say, $A$ which, by necessity, satisfies

(2)

$x^{a} = A,$ or $x = A^{1/a}.$

It is important to note that $A$ may be different from $y!$ In fact the function $f(z) = z^{1/z}$ is defined for all positive $z,$ has a maximum at $z = e,$ is monotone increasing for $z \lt e$ and is monotone decreasing for $z \gt e.$

This means that, for $1 \lt x \lt e^{1/e},$ the equation $y^{1/y} = x$ has two roots: one is less, the other is greater, than $e.$ For example, for $x = \sqrt{2},$ (1) has two solutions: $y = 2$ and $y = 4.$ (This is because $4^{1/4} = 2^{1/2}.$)

The sequence ${s_{n}}$ results if one attempts to solve (1) by an iterative procedure.

(3)

$s_{1} = 1,$ $s_{n+1} = g(s_{n}),$

where $g(s) = x^{s}.$ The derivative $g'(s) = dg(s)/ds$ is found to be

$g'(s) = \mbox{ln}(x)\cdot x^{s} = \mbox{ln}(x)\cdot g(s).$

If $x$ and $s$ are related via (1), i.e., if $x^{s}=s,$ then $g'(s) = (\mbox{ln}(s)/s\cdot s = \mbox{ln}s,$ which is greater or less than $1$ depending as to whether $s$ is greater or less than $e.$ If $|g'(s)| \gt 1,$ point $s$ is a repeller for the function $g(s),$ while for $|g'(s)| \lt 1,$ point $s$ is an attractor.

Note: years after this page was written, I submitted a link to this page as an answer to a question posed by Steven Strogatz on twitter. Thankfully, Steven pointed out that my answer was incomplete. Vacuously, the sequence $s_{n}$ converges also for $x = 1.$ More interestingly, the sequence converges for $e^{-e} \lt x \lt 1;$ although the nature of the convergence is different: the odd terms are monotone increasing, while the sequence of even terms is monotone decreasing. Both, though, have the same limit.

The inequality $|g'(s)| = |\mbox{ln}(s)| \lt 1$ is a prerequisite for convergence in both cases and is equivalent to $1/e \lt s \lt e.$ Further, $x(1/e)=(1/e)^e=e^{-e},$ while $x(e)=e^{1/e}.$ Since $x(s)$ is monotone increasing for $s \lt e,$ the two values define the interval - $(e^{-e}, e^{1/e})$ - of those $x$ for which the sequence $\{s_{n}\}$ converges, and the "infinite" makes sense.

References

P. Winkler, Mathematical Puzzles: A Connoisseur's Collection, A K Peters, 2004

71535432

xx3 = 3

References

x^x³ = 3