The Weierstrass Substitution
A standard way to calculate \(\int{\frac{dx}{1+\text{sin}x}}\) is via a substitution \(u=\text{tan}(x/2)\). As I'll show in a moment, this substitution leads to
\( \begin{align} \text{sin}x&=\frac{2u}{1+u^2} \\ \text{cos}x&=\frac{1-u^2}{1+u^2} \\ \text{tan}x&=\frac{2u}{1-u^2} \\ dx&=\frac{2du}{1+u^2} \end{align} \)
Using these,
\( \begin{align} \int{\frac{dx}{1+\text{sin}x}}&=\int{\frac{1}{1+2u/(1+u^{2})}\frac{2}{1+u^2}du} \\ &=\int{\frac{2du}{1+2u+u^2}} \\ &=\int{\frac{2du}{(1+u)^2}} \\ &=-\frac{2}{1+u}+C \\ &=-\frac{2}{1+\text{tan}(x/2)}+C. \end{align} \)
The method is known as the Weierstrass substitution. It applies to trigonometric integrals that include a mixture of constants and trigonometric function. H. Anton, though, warns the student that the substitution can lead to cumbersome partial fractions decompositions and consequently should be used only in the absence of finding a simpler method.
For another example,
\( \begin{align} \int{\frac{dx}{\text{sin}x+\text{tan}x}}&=\int{\frac{1}{\frac{2u}{1+u^2}+\frac{2u}{1-u^2}}\frac{2}{1+u^2}du} \\ &=\int{\frac{2(1-u^{2})}{2u}du} \\ &=\int{(\frac{1}{u}-u)du} \\ &=\text{ln}|u|-\frac{u^2}{2} + C \\ &=\text{ln}|\text{tan}(x/2)|-\frac{\text{tan}^2(x/2)}{2} + C. \end{align} \)
Now, let's return to the substitution formulas. It's not difficult to derive them using trigonometric identities. But here is a proof without words due to Sidney Kung:
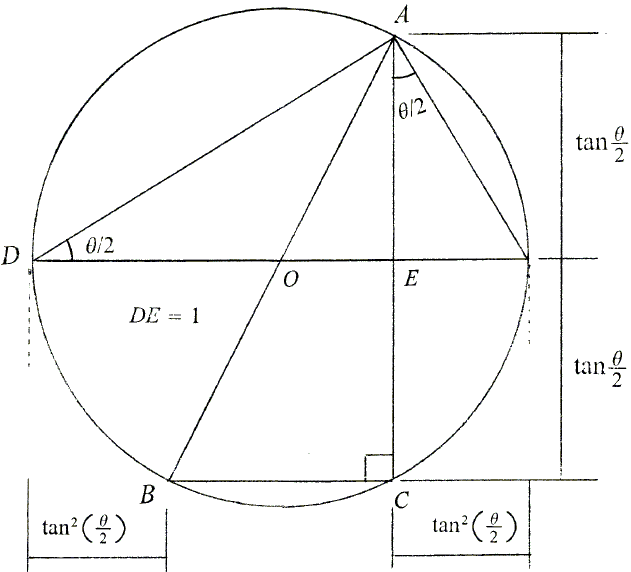
The diagram is suggestive of
\(\text{sin}\theta=\frac{AC}{AB}=\frac{2u}{1+u^2}\) and \(\text{cos}\theta=\frac{BC}{AB}=\frac{1-u^2}{1+u^2}\).
Finally, it must be clear that, since \(\text{tan}x\) is undefined for \(\frac{\pi}{2}+k\pi\), \(k\) any integer, the substitution is only meaningful when restricted to intervals that do not contain those values, e.g., for \(-\pi\lt x\lt\pi\).
References
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73581842
