Constrained Inequality with Reciprocals
Problem
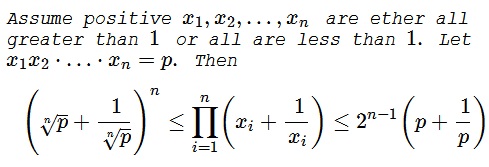
Solution 1
By Hölder's inequality, we have for the left inequality
$\displaystyle\prod_{k=1}^n\left(x_k+\frac{1}{x_k}\right)\ge\left(\prod_{k=1}^n\sqrt[n]{x_k}+\frac{1}{\displaystyle\prod_{k=1}^n\sqrt[n]{x_k}}\right)^n=\left(\sqrt[n]{p}+\frac{1}{\sqrt[n]{p}}\right)^n.$
For the right inequality, let $x_k\ge 1,\,$ $k=1,2,\ldots,n.\,$ Denote $x_k=e^{y_{k}},\,$ with $y_k\ge 0.\,$ Clearly, $\displaystyle\sum_{k=1}^ny_k=\ln p.\,$ We need to prove that
$\displaystyle\sum_{k=1}^n\ln (e^{y_k}+e^{-y_k})\le (n-1)\ln 2+\ln \left(e^{\ln p}+e^{-\ln p}\right).$
Obviously, the function $f(x)=e^{\ln x}+e^{-\ln x}\,$ is convex on $(0,\infty ).\,$ Also, the sequence $(\ln p, 0, 0,\ldots, 0)\,$ majorizes a properly ordered sequence $(y1,y_2,\ldots,y_n),\,$ so, with a reference to Karamata's inequality,
$\displaystyle\sum_{k=1}^nf(y_k)\le (n-1)f(0)+f(\ln p).$
Solution 2
We employ Hölder's inequality, as in Solution 1, to prove the left inequality. For the right one, we use complete induction.
For $n=1,\,$ there's nothing to prove. For $n=2,\,$ we need to show that $\displaystyle\left(x+\frac{1}{x}\right)\left(y+\frac{1}{y}\right)\le 2\left(xy+\frac{1}{xy}\right)\,$ which is equivalent to $\displaystyle\left(x-\frac{1}{x}\right)\left(y-\frac{1}{y}\right)\ge 0.\,$ The latter is true whenever both $x,y\ge 1\,$ or $x,y\le 1.$Assume that the inequality holds for all $n\le m,\,$ some $m\ge 2,$ i.e., given that $\displaystyle\prod_{k=1}^nx_k=p\,$ and either all $x_k\ge 1\,$ or all $x_k\le 1,\,$ then $\displaystyle\prod_{k=1}^n \left( x_{k}+\frac{1}{x_{k}} \right) \le 2^{n-1} \left( p+\frac{1}{p} \right).\,$ We have to prove that inequality holds for $n=m+1.$
So given $x_k,\,$ $k=1,\ldots,m+1,\,$ either all greater or all less than $1,\,$ we have
$\displaystyle\begin{align} \prod_{k=1}^{m+1}\left(x_k+\frac{1}{x_k}\right) &= \prod_{k=1}^{m-1}\left(x_k+\frac{1}{x_k}\right)\left(x_m+\frac{1}{x_m}\right)\left(x_{m+1}+\frac{1}{x_{m+1}}\right)\\ &\le 2^{m-2}\left(\prod_{k=1}^{m-1}x_k+\frac{1}{\displaystyle\prod_{k=1}^{m-1}x_k}\right)\cdot 2\left(x_mx_{m+1}+\frac{1}{x_mx_{m+1}}\right)\\ &\le 2^{m-1}\left(\prod_{k=1}^{m-1}x_k+\frac{1}{\displaystyle\prod_{k=1}^{m-1}x_k}\right)\left(x_mx_{m+1}+\frac{1}{x_mx_{m+1}}\right)\\ &\le 2^{m}\left(\prod_{k=1}^{m+1}x_k+\frac{1}{\displaystyle\prod_{k=1}^{m+1}x_k}\right). \end{align}$
Solution 3
The left inequality follows from Huygens inequality:
$\displaystyle\sqrt[n]{\prod_{k=1}^n(a_k+b_k)}\ge\sqrt[n]{\prod_{k=1}^na_k}+\sqrt[n]{\prod_{k=1}^nb_k}$
by raising to the $n\text{-th}\,$ power and setting $a_k=x_k\,$ and $\displaystyle b_k=\frac{1}{x_k},\,$ $k\in\overline{1,n}.$
For the right inequality we need the following result from the article by Doring Marghidanu, Inegalitati pentru n-upluri aflate in relatie de dominare, Revista de matematica si informatica (Constanta, pp 4-5, Anul XII, nr. 2, martie, 2012):
Theorem
If $a_i,b_i\ge 0\,$ and $a_i\ge b_i\,$ (or $b_i\ge a_i,\,$ for any $i\in\overline{1,n},\,$ then
$\displaystyle\prod_{k=1}^n(a_k+b_k)\le 2^{n-1}\left(\prod_{k=1}^na_k+\prod_{k=1}^nb_k\right).\,$
Note that the problem is solved by choosing $a_k=x_k\,$ and $\displaystyle b_k=\frac{1}{x_k},\,$ $k\in\overline{1,n}.$
Proof of the theorem
We prove the theorem by mathematical induction.
For $n=2,\,$ the inequality becomes $(a_1+b_1)(a_2+b_2)\le 2(a_1a_2+b_1b_2),\,$ which is equivalent to the obvious under the conditions of the theorem $(a_1-b_1)(a_2-b_2)\ge 0.$
Suppose the inequality $\displaystyle\prod_{k=1}^n(a_k+b_k)\le 2^{n-1}\left(\prod_{k=1}^na_k+\prod_{k=1}^nb_k\right)\,$ and prove that $\displaystyle\prod_{k=1}^{n+1}(a_k+b_k)\le 2^{n}\left(\prod_{k=1}^{n+1}a_k+\prod_{k=1}^{n+1}b_k\right),\,$ with $a_i\ge b_i\,$ or $b_i\ge a_i,\,$ for all $i\in\overline{1,n}.$
But
$\displaystyle\begin{align} \prod_{k=1}^{n+1}(a_k+b_k)&\le 2^{n}\left(\prod_{k=1}^{n}(a_k+b_k)\right)\\ &\le \left(\prod_{k=1}^na_k+\prod_{k=1}^nb_k\right)(a_{n+1}+b_{n+1})\\ &\le 2^{n-1}\left(\prod_{k=1}^na_k+\prod_{k=1}^nb_k\right)(a_{n+1}+b_{n+1}). \end{align}$
It remains to be shown that $\displaystyle 2^{n-1}\left(\prod_{k=1}^na_k+\prod_{k=1}^nb_k\right)(a_{n+1}+b_{n+1})\le 2^{n}\left(\prod_{k=1}^{n+1}a_k+\prod_{k=1}^nb_k\right).\,$ This is equivivalent to,
$\displaystyle\left(\prod_{k=1}^na_k+\prod_{k=1}^nb_k\right)(a_{n+1}+b_{n+1})\le 2\left(\prod_{k=1}^{n+1}a_k+\prod_{k=1}^nb_k\right).$
And we have a sequence of equivalences:
$\displaystyle\begin{align} &\left(\prod_{k=1}^na_k+\prod_{k=1}^nb_k\right)(a_{n+1}+b_{n+1})\le 2\left(\prod_{k=1}^{n+1}a_k+\prod_{k=1}^nb_k\right)\\ &\Longleftrightarrow \prod_{k=1}^{n+1}a_k+\left(\prod_{k=1}^na_k\right)b_{n+1}+a_{n+1}\left(\prod_{k=1}^nb_k\right)+\prod_{k=1}^{n+1}a_k\le 2\prod_{k=1}^na_k+2\prod_{k=1}^nb_k\\ &\Longleftrightarrow\left(\prod_{k=1}^na_k\right)b_{n+1}+a_{n+1}\left(\prod_{k=1}^nb_k\right)\le \prod_{k=1}^na_k+\prod_{k=1}^nb_k\\ &\Longleftrightarrow\left(\prod_{k=1}^na_k\right)(a_{n+1}-b_{n+1})-\left(\prod_{k=1}^nb_k\right)(a_{n+1}-b_{n+1})\ge 0\\ &\Longleftrightarrow \left(\prod_{k=1}^na_k-\prod_{k=1}^nb_k\right)(a_{n+1}-b_{n+1})\ge 0 \end{align}$
which completes the proof by induction. Equality is obtained when $a_i=b_i,\,$ $i\in\overline{1,n}.$
Acknowledgment
Dorin Marghidanu has kindly posted the problem at the CutTheKnotMath facebook page. Solution 1 is by Leo Giugiuc; Solution 3 is by Dorin Marghidanu.
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73497320
