A Property of Number 4

Number $4$ has an interesting while easily verifiable property:

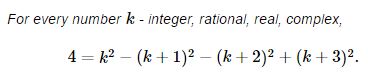
The freedom of choosing $k$ can be used to show that number $0$ also has an interesting and easily verifiable property:

For every number $k$ - integer, rational, real, complex,

$\begin{align} 0=k^{2}&-(k+1)^{2}-(k+2)^{2}+(k+3)^{2}\\ &-(k+4)^{2}+(k+5)^{2}+(k+6)^{2}-(k+7)^{2}. \end{align}$

This is used to answer a problem considered by Paul Erdös and Janos Surányi in 1960:

Every integer $n$ can be represented in infinitely many ways as

(1)

$n=\pm 1^{2}\pm 2^{2}\pm 3^{2}\pm \cdots \pm k^{2}.$

For a proof, observe that if number $n$ admits a representation (1), then so does number $n+4$ whose representation can be obtained from that of $n$ by appending $(k+1)^{2}-(k+2)^{2}-(k+3)^{2}+(k+4)^{2}.$ From the above property of $0$ it then follows that both $n$ and $n+4$ have an infinite number of such representations. Clearly, it is sufficient to consider only positive integers. Representations of the negative ones are obtained by reversing the signs of their absolute value. Thus to solve Erdös and Surányi's problem we only need to establish that some four consecutive numbers admit a representation as an algebraic sum of the squares several consecutive integers. That is simple:

$\begin{align} 1&=1^{2},\\ 2&=-1^{2}-2^{2}-3^{2}+4^{2},\\ 3&=-1^{2}+2^{2},\\ 4&=1^{2}-2^{2}-3^{2}+4^{2}. \end{align}$

References

S. Savchev, T. Andreescu, Mathematical Miniatures, MAA, 2003, p 47

71535777