The power of substitution
solving an equation in a right triangle

Here's a problem due to Maria-Elena Panaitopol posted by Leo Giugiuc, along with a solution (Solution 1), at the CutTheKnotMath facebook page. Solution 2 is due to Alexander Price.

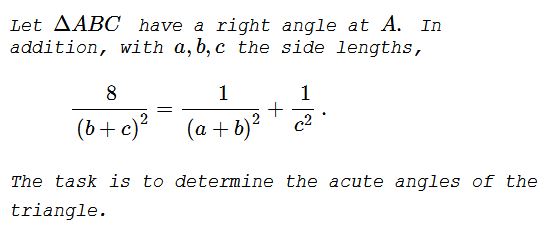
The power of substitution: solving an equation in a right triangle

Solution

Let $\Delta ABC\;$ have a right angle at $A.\;$ In addition, with $a,b,c$ the side lengths,

$\displaystyle\frac{8}{(b+c)^2}=\frac{1}{(a+b)^2}+\frac{1}{c^2}.\;$

The task is to determine the acute angles of the triangle.

Solution 1

WLOG, $a=1,\;$ $b=\cos t,\;$ $c=\sin t,\;$ where $\displaystyle 0\lt t\lt\frac{\pi}{2}.\;$ With this substitution, the given equation becomes $\displaystyle\frac{4}{(\cos t+\sin t)^2}=\frac{1}{(1+\cos t)\sin^2t},\;$ which is equivalent to $\displaystyle\frac{4}{(1+\cot t)^2}=\frac{1}{1+\cos t}.$

Denote $\cot t=x.\;$ Naturally, $x\gt 0\;$ and $\displaystyle\cos t=\frac{x}{\sqrt{1+x^2}},\;$ and the latter is equivalent to

$\displaystyle\frac{4}{(1+x)^2}=\sqrt{1+x^2}(\sqrt{1+x^2}-x).$

Finally, introduce $y=\sqrt{1+x^2}-x\;$ such that $0\lt y\lt 1\;$ and $\displaystyle x=\frac{1-y^2}{y}.\;$ After straightforward calculations, this reduces to

$(y^2-4y+1)(y^4+2y^2+8+1)=0.$

The second factor is positive for $y\in (0,1),\;$ so we only need to solve $y^2-4y+1=0.\;$ This has only one solution on $(0,1):\;$ $y=2-\sqrt{3}.\;$ Then $x=\sqrt{3},\;$ implying $\displaystyle t=\frac{\pi}{6},\;$ i.e., $\displaystyle B=\frac{\pi}{3}\;$ and $\displaystyle C=\frac{\pi}{6}.\;$ A nice triangle.

Solution 2

Bear in mind that, according to the Pythagorean theorem, $a^2=b^2+c^2.\;$ We can write

$\displaystyle\begin{align} \frac{8}{(b+c)^2}&=\frac{1}{(a+b)^2}+\frac{1}{c^2}\\ &=\frac{1}{(a+b)^2}+\frac{1}{a^2-b^2}\\ &=\frac{2a(a+b)}{(a+b)^2(a^2-b^2)}\\ &=\frac{2a}{(a+b)c^2}. \end{align}$

On the other hand, $\displaystyle\frac{1}{(b+c)^2}=\frac{1}{a^2+2bc}.\;$ Equating the two end results gives

$4ac^2+4bc^2=a^3+2abc,$

which is the same as

$2bc(2c-a)=a(a^2-4c^2)=a(a+2c)(a-2c).$

Note now that, unless $a-2c=0,\;$ the two sides will differ in signs. Therefore, necessarily $a=2c,\;$ which exactly means that $\displaystyle \angle C=\frac{\pi}{6}\;$ and, as a consequence, $\displaystyle \angle B=\frac{\pi}{3}.\;$

71546804

The power of substitution solving an equation in a right triangle

Solution 1

Solution 2

The power of substitution
solving an equation in a right triangle