An Exercise without Calculating Aids
Problem
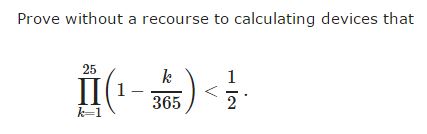
Solution 1
Using the AM-GM inequality,
$\displaystyle\begin{align} \prod_{k=1}^{25}\left(1-\frac{k}{365}\right)&\le \left[\frac{1}{25}\sum_{k=1}^{25}\left(1-\frac{k}{365}\right)\right]^{25}\\ &=\left[\frac{1}{25}\sum_{k=1}^{25}\frac{365-k}{365}\right]^{25}\\ &=\left[\frac{1}{25}\cdot 25\frac{340+364}{2\cdot 365}\right]^2=\left(\frac{352}{365}\right)^{25}\\ &=\left(1-\frac{13}{365}\right)^{25}\\ &\lt 1-25\frac{13}{365}+\frac{25\cdot 24}{2}\left(\frac{13}{365}\right)^{25}\\ &=1-\frac{65}{73}+\frac{25\cdot 12\cdot 13^2}{5^2\cdot 73^2}\\ &=\frac{8\cdot 73+12\cdot 13^2}{73^2}\\ &=\frac{584+2028}{5329}=\frac{2592}{5329}\\ &\lt\frac{1}{2}, \end{align}$
where, at an intermediate step, we used the fact that the terms in the binomial expansion of $\displaystyle\left(1-\frac{13}{365}\right)^{25}\,$ are decreasing in the absolute value, so that the first three terms bound the whole from above. To see that this is so suffice it to check that $\displaystyle\frac{13}{365}{25\choose k+1}\lt {25\choose k}.\,$ This is equivalent to showing $\displaystyle\frac{13}{365(k+1)}\lt\frac{1}{25-k},\,$ or, $13\cdot 25-365\lt 378k.\,$ The number on the left is negative, so that the inequality holds for all relevant $k.$
Solution 2
We know the Taylor siries for $y=\ln (1-x)\,$ is
$\displaystyle \ln (1-x)=-x-\frac{x^2}{2}-\frac{x^3}{3}-\ldots,$
so that, with $k\gt 0,$
$\displaystyle \ln(1-\frac{k}{365})\lt -\frac{k}{365}.$
From here,
$\displaystyle\begin{align} \ln \left(\prod_{k=1}^{25}\left(1-\frac{k}{365}\right)\right)&\lt -\sum_{k=1}^{25}\frac{k}{365}\\-\frac{325}{365} &=-\frac{25\cdot 26}{2\cdot 365}=-\frac{325}{365}\\ &\lt -\ln (2). \end{align}$
Solution 3
We start as in Solution 2 and reach $\displaystyle -\frac{325}{365}.\,$ To continue,
$\displaystyle -\frac{65}{73} \lt -0.8.$
Thus it follows that
$\displaystyle\begin{align} e^{-0.8} &= 1+(-0.8)+\frac{1}{2}(-0.8)^2+\frac{1}{3!}(-0.8)^3+\frac{1}{4!}(-0.8)^4+\ldots\\ &\lt 1+(-0.8)+\frac{(-0.8)^2}{2}+\frac{(-0.8)^3}{6}+\frac{(-0.8)^4}{24}\\ &=0.2+0.32-\frac{0.256}{3}+\frac{0.0512}{3}\\ &\lt 0.52-0.068=0.452\\ &\lt .5 \end{align}$
Acknowledgment
This is an old problem from a student competition offered at the time when no handheld devices had yet penetrated the Soviet reality. Solution 2 is by Nassim Nicholas Taleb; Solution 3 is by Mike Lawler.
Remark
It's more cumbersome, but not exceedingly so, to manually verify that $\displaystyle\prod_{k=1}^{23}\left(1-\frac{k}{365}\right)\lt\frac{1}{2}.\,$ The calculations lead to $\displaystyle\frac{65377}{133225}.\,$ This is the probability that $23\,$ random people all have distinct birthdays. Clearly that is less than half, implying that in a random group of $23\,$ people there will be two with the same birthday with the probability higher than $50%.$
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73518182
