A Middle School Problem from a Moscow Olympiad

Here is Problem 29 from the 20th Moscow University Mathematics Olympiad (1957) intended for the 8th grade which is an equivalent of the US middle or junior high school.

Solve the system of equations

\( \begin{align} \frac{2x_{1}^{2}}{1+x_{1}^{2}} & = x_{2}, \\ \frac{2x_{2}^{2}}{1+x_{2}^{2}} & = x_{3}, \\ \frac{2x_{3}^{2}}{1+x_{3}^{2}} & = x_{1}. \\ \end{align} \)

Solution

Solve the system of equations

\( \begin{align} \frac{2x_{1}^{2}}{1+x_{1}^{2}} & = x_{2}, \\ \frac{2x_{2}^{2}}{1+x_{2}^{2}} & = x_{3}, \\ \frac{2x_{3}^{2}}{1+x_{3}^{2}} & = x_{1}. \\ \end{align} \)

Looking at the problem, the first thing that came to mind is that a solution should make use of the circular symmetry of the three equations and probably some of the properties of the function \(f(x)=\frac{2x^{2}}{1+x^{2}}\) because (in terms of this function) the system can be rewritten as

\( \begin{align} f(x_{1}) = x_{2}, \\ f(x_{2}) = x_{3}, \\ f(x_{3}) = x_{1}. \\ \end{align} \)

The existence of three distinct numbers that satisfy the system would amount to an iterative 3-cycle, which makes it worth to inspect the graph of function \(f\):

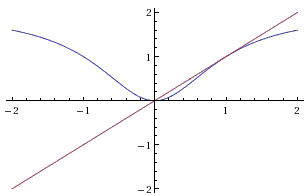
a graph of function f(x)=2x^2/(1+x^2)

The graph is tangent to the \(x\)-axis at the origin and the diagonal \(y=x\) at \((1,1)\). We can see that by solving the equation for the stationary points of function \(f\): \(f(x)=x\). Factoring one \(x\) out and multiplying by the denominator leaves - after the factorization - a simple equation:

\(x(x - 1)^2=0\),

with a single root at \(x=0\) and a double root at \(x=1\). The graph makes it is clear that the iterations \(x_{k+1}=f(x_{k})\) that start in the interval \((0,1)\) converge to \(0\), while the iterations that start to the right of \(x=1\) converge to \(1\). In both cases the convergence is monotone and the limit is never reached. Which leads to the conclusion that the system could not have solutions with distinct \(x\)'s and, therefore, has only two solutions, namely, \((0, 0, 0)\) and \((1, 1, 1)\). In passing, the same could be said of a similar system of any number of equations.

A solution I found in a Russian collection of olympiad problems requires more ingenuity.

First observe that if one of the unknowns is \(0\) so are the others. This gives one solution \((0, 0, 0)\) and allows to assume that none of the unknowns is \(0\). Under this condition the system can be rewritten in terms of reciprocals \(y_{I}=1/x_{I}\):

\( \begin{align} 2y_{2} = 1+y_{1}^{2}, \\ 2y_{3} = 1+y_{2}^{2}, \\ 2y_{1} = 1+y_{3}^{2}. \\ \end{align} \)

These equation can be added to produce

\((1-y_{1})^{2}+(1-y_{2})^{2}+(1-y_{3})^{2}=0\),

which admits a unique solution \((1,1,1)\). This method, too, works for any number of equations (and unknowns.)

71542518