Divergence of the Harmonic Series (Details)
Problem

Solution 1
We know that the sequence $\gamma_n=H_n-\ln (n+1)\,$ is strictly increasing and all it terms are positive. Hence,
$\displaystyle H_{10^{10}-1}-\ln 10^{10}\gt 0,$
implying $\displaystyle H_{10^{10}-1}\gt 10\ln 10\gt 9.$
Solution 2
$\displaystyle\begin{align} H_{10^n-1} &= \sum_{k=1}^{10^n-1}\frac{1}{k}=\sum_{i=0}^{n-1}\sum_{k=10^i}^{10^{i+1}-1}\frac{1}{k}\\ &\gt \sum_{i=0}^{n-1}(10^{i+1}-10^i)\frac{1}{10^{i+1}-1}\gt \sum_{i=0}^{n-1}10^{i}\cdot 9\frac{1}{10^{i+1}}\\ &=\sum_{i=0}^{n-1}\frac{9}{10}=n\cdot\frac{9}{10}. \end{align}$
For $n=10,\,$ $\displaystyle H_{10^n-1}\gt 9,\,$ i.e., $\displaystyle H_{\underbrace{99\ldots 99}_{n\;digits}}\gt 9.$
Solution 3
$\displaystyle\begin{align} H_{2^n} &= \sum_{k=2}^{2^n}\frac{1}{k}=\sum_{i=1}^{n}\sum_{k=2^{i-1}+1}^{2^i}\frac{1}{k}\\ &\gt \sum_{i=0}^{n-1}(2^{i}-2^{i-1})\frac{1}{2^{i}}\gt \sum_{i=0}^{n-1}\frac{1}{2}\\ &=n\cdot\frac{1}{2}. \end{align}$
For $n=18,\,$ $\displaystyle H_{2^n}\gt 9.\,$ Now, the problem will be solved if we can show that $2^{18}\le 10^{10}.\,$ This is indeed so because $2^9=512\lt 10^3\,$ such that $2^{18}=(2^9)^2\lt (10^3)^2=10^6\lt 10^{10}.$
Solution 4
We set $\displaystyle I_n=\int_1^n\frac{dx}{x}=\ln (n)\,$ show visually and formally from the properties of the Riemann integration that $H_n\ge I_n.$
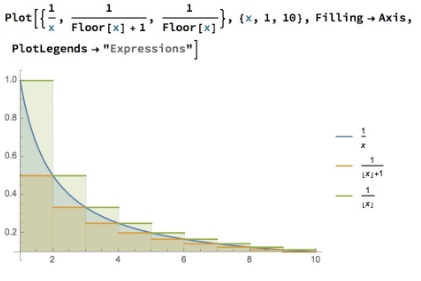
$H_n\gt \ln (n),\,$ $H_{10^6}\ge \ln (10^6) = 6(\ln (2)+\ln (5))\gt 9.$
We can continue from here. Graph gets us the obvious inequality and both truth and justice prevail!
Acknowledgment
Dorin Marghidanu has kindly posted the problem at the CutTheKnotMath facebook page. Solution 1 is by Leo Giugiuc; Solution 2 is by Dorin Marghidanu; Solution 4 is by Nassim Nicholas Taleb.
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73576651
