What 1, 6, and 14 Have to Do with 5?
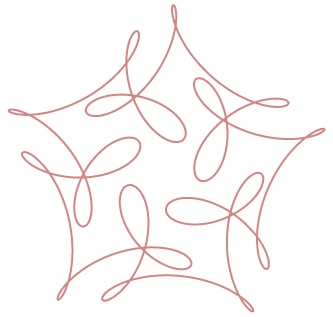
If you have no experience dealing with the sort of graphs similar to the one above, you may be surprised by the kind of a function that underlies its definition. Why so?
It is clear the graph has a five-fold symmetry which means that there is a point - the center of the symmetry - such that rotations of the graph by $72^{\circ}$ around that point coincide (point-wise) with the graph itself. Invoking complex numbers, if $f:\;\mathbb{R}\rightarrow\mathbb{C}$ is a complex-valued function of a real argument, then the condition that its graph has a five-fold symmetry may be expressed as
$\displaystyle f(t+\frac{2\pi}{5})=e^{\frac{2\pi}{5}i}f(t).$
This said, what perhaps is surprising is that the graph above is defined by the function
$\displaystyle\begin{align} f(t)&=e^{it}+e^{6it}/2+ie^{-14it}/3\\ &=\left(\cos t+\frac{1}{2}\cos 6t+\frac{1}{3}\sin 14t,\;\sin t+\frac{1}{2}\sin 6t+\frac{1}{3}\cos 14t\right). \end{align}$
The first component of the function - $e^{it}$ - defines the unit circle and, with the argument $t$ thought as evolving, it may be looked at as describing the motion of a point on the circle with period $2\pi.$ Similarly, the second component - $e^{6it}/2$ - defines the motion over a circle of radius $1/2$ with period of $2\pi/6=\pi /3,$ while the third component has a period of $\pi /7.$ How the combination of the three motions leads to a five-fold graph? Before giving a general statement that answers this question, let's verify that the five-fold symmetry of the graph above is not a visual illusion.
$\displaystyle\begin{align} f(t+\frac{2\pi}{5}) &= e^{i(t+\frac{2\pi}{5})}+e^{6i(t+\frac{2\pi}{5})}/2+ie^{-14i(t+\frac{2\pi}{5})}/3\\ &= e^{i\frac{2\pi}{5}}\cdot e^{it}+e^{i\frac{12\pi}{5}}\cdot e^{6it}/2+ie^{-i\frac{28\pi}{5}}\cdot e^{-14it}/3\\ &= e^{i\frac{2\pi}{5}}\left( e^{it}+e^{i\frac{10\pi}{5}}\cdot e^{6it}/2+ie^{-i\frac{30\pi}{5}}\cdot e^{-14it}/3\right)\\ &= e^{i\frac{2\pi}{5}}\left( e^{it}+e^{2\pi i}\cdot e^{6it}/2+ie^{-6\pi i}\cdot e^{-14it}/3\right)\\ &= e^{i\frac{2\pi}{5}}\left( e^{it}+e^{6it}/2+ie^{-14it}/3\right)\\ &=e^{i\frac{2\pi}{5}}f(t). \end{align}$
Here's the general statement:
Theorem
Suppose that $m$ and $k$ are integers and that all the frequency numbers $n_{j}$ in the finite sum
$f(t)=a_{1}e^{n_{1}it}+a_{2}e^{n_{2}it}+\ldots+a_{M}e^{n_{M}it}$
have
$n_{j}\equiv k\;(\text{mod}\; m).$
Then, for any choice of the complex coefficients $a_{j},$ $f$ satisfies the symmetry condition
(*)
$\displaystyle f(t+\frac{2\pi}{m})=e^{\frac{2k\pi i}{m}}f(t).$
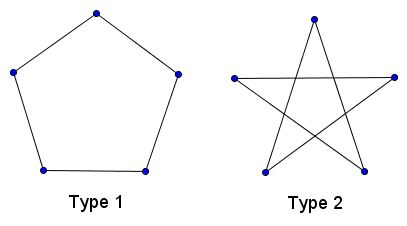
The appearance of $k$ in the right-hand side of the symmetry condition warrants an explanation. The simplest one is to point to the analogy with classification of polygons. In the diagram below two polygons, the first denoted $\{5/1\},$ the second $\{5/2\},$ correspond to curves with $5$-fold symmetry - the first of type $1,$ the second of type $2.$
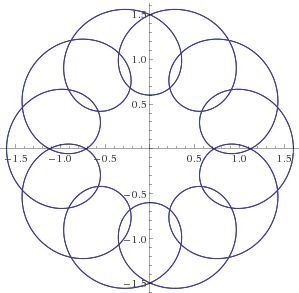
In general, the coefficient $k$ in (*) defines the type of the $m$-fold symmetry. Here are two examples: the first is a $10$-fold symmetry of type $1,$
the next one illustrates $10$-fold symmetry of type $3.$
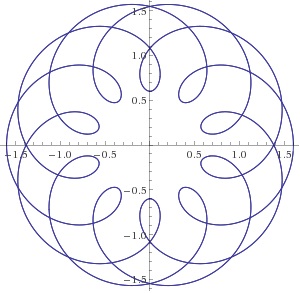
A curve showing $10$-fold symmetry of type $2$ has in fact $5$-fold symmetry and overlaps itself twice. This is why it is common in devising various curves request $m$ and $k$ to be mutually prime.
References
- F. A. Harris, Creating Symmetry: The Artful Mathematics of Wallpaper Paterns, Princeton University Press, 2015
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny
73574905
