A System of Equations in Determinants

Dan Sitaru has kindly posted the following problem from the Romanian Mathematical Magazine and its solution by Ravi Prakash at the CutTheKnotMath facebook page:

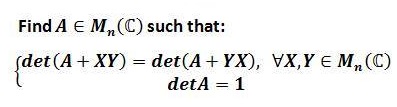
Solution

Let $E_{ij}=(\delta_{ij})\;$ be the matrix with all elements zero, except for the one in $i-\text{s}\;$ row and $j-\text{s}\;$ column which is $1.\;$ Note that

$E_{ij}E_{rs}=\begin{cases}E_{is},& \text{if}\;j=r\\ 0, & \text{otherwise} \end{cases}$

Consider $X=\alpha E_{ik},\;$ $\alpha\in\mathbb{C}\;$ and $Y=E_{ks};\;$ $XY=\alpha E_{is},\;$ $YX=0\;$ unless $i=s\;$ and $X=E_{ii},\;$ otherwise. Thus, taking $i\ne s,\;$ $\det(A+\alpha E_{is})=\det(A).\;$ Now using the minor expansion of the determinant,

$\displaystyle\begin{align} \det(A+\alpha E_{is}) &= \sum_{j=1}^{n}(a_{ij}+\alpha\delta_{ij})M_{ij}(-1)^{i+j}\\ &=\sum_{j=1}^{n}a_{ij}M_{ij}(-1)^{i+j}+\alpha M_{is}(-1)^{i+s}\\ &=\det(A)+\alpha M_{is}(-1)^{i+s}\\ \end{align}$

Since this equals $\det(A)\;$ and $\alpha\;$ is arbitrary, $M_{is}=0,\;$ $i\ne s.\;$ Then from

$\displaystyle\det(A)=\sum_{j=1}^{n}a_{ij}M_{ij}(-1)^{i+j}=a_{ii}M_{ii}$

it follows that $a_{ii}M_{ii}=1,\;$ for all $i=1,\ldots,n.$ In particular, for $i=1,\ldots,n,$ $a_{ii}\ne 0\;$ and $M_{ii}\ne 0.$

On the other hand, the choice $X=E_{rs}\;$ and $Y=E_{sr}\;$ leads to

$\displaystyle\det(A)+\alpha M_{rr}=\det(A)+\alpha M_{ss}$

so that all diagonal minors of $A\;$ are equal and, as a consequence, so are all its diagonal elements: $a_{ii}=\lambda,\;$ for $i=1,\ldots,n\;$ and a fixed $\lambda\in\mathbb{C}.$

Next, for $i_1\ne i_2,\;$

$\displaystyle 0=\sum_{j=1}^{n}a_{i_1j}M_{i_2j}(-1)^{i_1+j}=a_{i_1i_2}M_{i_2i_2},$

implying that all off-diagonal elements of $A\;$ are zero: $a_{i_1i_2}=0,\;$ for $i_1\ne i_2.$ Thus $A=\lambda E,\;$ where $E\;$ is the unit matrix. Finally, $1=\det(A)=\lambda^n\;$ implies $\lambda^n=1,\;$ i.e., $\lambda\;$ is a root of unity.

71547045