A Sum

Dorin Marghidanu
April 9, 2016

Problem

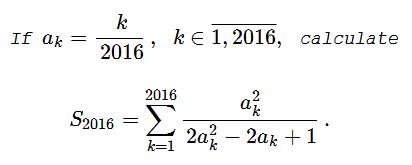
Solution

We observe that

$\displaystyle 1-a_k=1-\frac{k}{2016}=\frac{2016-k}{2016}=a_{2016-k}.$

Hence, $a_k+a_{2016-k}=1,\;$ $1\le k\le 2015.$ If $\displaystyle t_k=\frac{a_k^2}{2a_k^2-2a_k+1},\;$ then for $k\in\overline{1,2015},\;$

$\displaystyle\begin{align} t_k &= \frac{a_k^2}{2a_k^2-2a_k+1}\\ &=\frac{a_k^2}{a_k^2+(1-a_k)^2}\\ &=\frac{a_k^2}{a_k^2+a_{2016-k}^2}. \end{align}$

Therefore, $\displaystyle t_{2016-k}=\frac{a_{2016-k}^2}{a_k^2+a_{2016-k}^2},\;$ $k\in\overline{1,2015}.\;$ It follows that for $k\in\overline{1,2015},\;$ $t_k+t_{2016-k}=1.\;$ Summing up,

$\begin{align} S_{2015} &= \sum_{k=1}^{2016}t_k\\ &=\left[(t_1+t_{2015})+(t_2+t_{2014})\right]+\ldots+(t_{1007}+t_{1009})\\ &=\sum_{k=1}^{1007}+t_{1008}+t_{2016}\\ &=1007+\frac{1}{2}+1\\ &=\frac{2017}{2}. \end{align}$

Generalization

If $\displaystyle a_k=\frac{k}{n},\;$ $k\in\overline{1,n},\;$ calculate

$\displaystyle S_{n}=\sum_{k=1}^{n}\frac{a_k^2}{2a_k^2-2a_k+1}.$

The solution in this case follows the previous one, with $2016\;$ replaced by $n,\;$ up to the last step where we have to distinguish between $n\;$ being odd or even, though in both cases $t_k+t_{n-k}=1,\;$ for $k\in\overline{1,n-1}.\;$ If $n=2m,$

$\displaystyle\begin{align} S_n&=S_{2m}\\ &=\sum_{k=1}^{2m}t_k\\ &=\left[(t_1+t_{2m-1})+(T_2+t_{2m-2})+\ldots+(t_{m-1}+t_{m+1})\right]+t_m+t_{2m}\\ &=(m-1)+\frac{1}{2}+1\\ &=\frac{2m+1}{2}. \end{align}$

For $n=2m+1,\;$ we have

$\displaystyle\begin{align} S_n&=S_{2m+1}\\ &=\sum_{k=1}^{2m+1}t_k\\ &=\left[(t_1+t_{2m})+(T_2+t_{2m-1})+\ldots+(t_{m}+t_{m+1})\right]+t_{2m+1}\\ &=m+1. \end{align}$

To sum up:

$\displaystyle S_n= \begin{cases} \frac{2m+1}{2},& if\;n=2m,\\ m+1, & if\;n=2m+1. \end{cases}$

In one word, $\displaystyle S_n=\frac{n+1}{2}.$

Another solution

We are going to use the well known trick that was employed years ago by young Gauss:

$\displaystyle\begin{align} S_{n} &=\sum_{k=0}^{n}\frac{a_k^2}{2a_k^2-2a_k+1}\\ &=\sum_{k=0}^{n}\frac{a_k^2}{a_k^2+(1-a_k)^2}\\ &=\sum_{k=0}^{n-1}\frac{a_k^2}{a_k^2+a_{n-k}^2}\\ &=\sum_{k=0}^{n}\frac{a_{n-k}^2}{a_{n-k}^2+a_k^2}. \end{align}$

It follows that

$\displaystyle\begin{align} 2S_{n} &=\sum_{k=0}^{n-1}\frac{a_k^2}{a_k^2+a_{n-k}^2}+\sum_{k=0}^{n}\frac{a_{n-k}^2}{a_{n-k}^2+a_k^2}\\ &=\sum_{k=0}^{n}\frac{a_k^2+a_{n-k}^2}{a_{n-k}^2+a_k^2}\\ &=n+1. \end{align}$

Therefore, $\displaystyle S_n=\frac{n+1}{2}.$