Cospherical Points

Leo Giugiuc has kindly communicated to me a problem from the Romanian Mathematical Magazine due to Dan Sitaru, along with his solution to the problem:

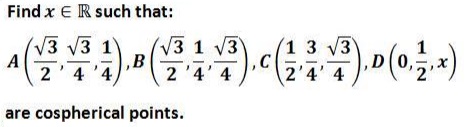
Cospherical Points

Solution

In the Euclidean 2D space any three distinct points are concyclic, unless they are collinear. In the Euclidean 3D space any four distinct points are cospherical, unless they are coplanar but not concyclic.

The three distinct points $A,B,C\;$ define a plane, say $\alpha\;$ and a circle, say $\omega.\;$ It is immediately verifiable that $A,B,C\in S,\;$ where $S\;$ denotes the unit sphere $x^2+y^2+z^2=1.\;$ In particular, $\omega=\alpha\cap S.$

The condition for the for the four points be coplanar is given by

$\displaystyle\left|\begin{array}{cccc} 2\sqrt{3} & \sqrt{3} & 1 & 1\\ 2\sqrt{3} & 1 & \sqrt{3} & 1\\ 2 & 3 & \sqrt{3} & 1\\ 0 & 2 & 4x & 1 \end{array}\right|=0.$

The equation implies $\displaystyle x=\frac{5}{4},\;$ i.e., $\displaystyle D=\left(0,\frac{1}{2},\frac{5}{4}\right),\;$ meaning $D\notin S\;$ and, therefore, $D\notin\omega.\;$ So, if $\displaystyle x=\frac{5}{4},\;$ $A,B,C,D\;$ are coplanar, but not cospherical. If $\displaystyle x\ne\frac{5}{4},\;$ then $A,B,C,D\;$ are not coplanar and, hence, are cospherical.

Thus the answer is $\displaystyle\mathbb{R}\setminus\left\{\frac{5}{4}\right\}.$

71537018