Four KnightsThe applet below presents an old puzzle. The board is a 3x3 part of the chessboard. The only allowed move is to drag a knight to another square following the usual chess rules. Of course, no two knights may occupy the same square. The purpose of the puzzle is to swap red and blue knights. On the right, 8 squares are arranged in a sequence. There is correspondence between the squares and knights on the two halves of the display. The sooner you grasp this relationship, the easier it will be for you to solve the puzzle.
The picture on the right shows all the legitimate knight moves. There is no way to reach the middle square. From all others there are exactly two legitimate moves. This observation permits unfolding the moves into a sequence of 8 squares as depicted in the right half of the applet. On the right all it takes to solve the problem is to shift knights in a selected (either will do) direction one after another. 
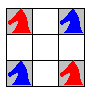
You can check whether you really understand the relationship between the two diagrams by answering the following questions. What is the minimum number of moves required to solve the puzzle? Is it possible starting with the original configuration to arrange the knights as depicted on the left?  |Contact| |Front page| |Contents| |Store| |Games| |Eye opener| Copyright © 1996-2012 Alexander Bogomolny |
| 40608030 |
