Probability in the World Series

The probability of winning the World Series in exactly $n$ games is

$\displaystyle P(n)=\frac{1}{2}\cdot\frac{1}{2^{n-1}}\cdot{n-1\choose 3}\cdot 2=\frac{1}{2^{n-1}}\cdot{n-1\choose 3}.$

because $\displaystyle \frac{1}{2}$ is the probability of winning the $n^{th}$ game, $\displaystyle {n-1\choose 3}/2^{n-1}$ is the probability of winning three games out of the previous $n-1,$ and there are two teams to choose from.

We have $\displaystyle P(4)=\frac{1}{8},$ $\displaystyle P(5)=\frac{1}{4},$ $\displaystyle P(6)=\frac{5}{16},$ $\displaystyle P(7)=\frac{5}{16}.$ The expectation $E$ is then

$\displaystyle E=4\cdot\frac{1}{8}+5\cdot\frac{1}{4}+6\cdot\frac{5}{16}+7\cdot\frac{5}{16}=\frac{93}{16}=5.8125.$

Form a Markov chain with absorbing states $\{11,15,16,19,20,22,23,24\}$ as below:

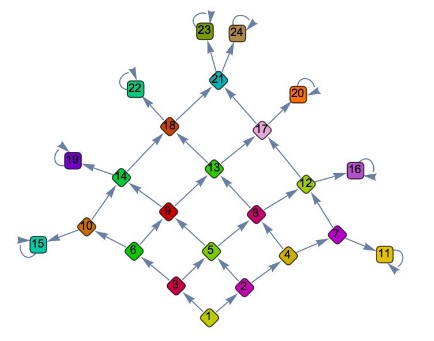
Those states are attained with probabilities $\displaystyle \{\frac{1}{16},\frac{1}{16},\frac{1}{8},\frac{1}{8},\frac{5}{32},\frac{5}{32},\frac{5}{32},\frac{5}{32}\}$ in $\{4,4,5,5,6,6,7,7\}$ games, respectively. Thus we obtain the expectation of

$\displaystyle \frac{1}{4}+\frac{1}{4}+\frac{5}{8}+\frac{5}{8}+\frac{30}{32}+\frac{30}{32}++\frac{35}{32}+\frac{35}{32}=5.8215.$

For the series to end in $n$ games ($n\geq 4$), the winning team has to win $3$ of the first $n-1$ games and the $n^{th}$ game. Moreover, either one of the two teams could be the winning team. Thus, the expected number of games is given by

$\displaystyle\begin{align} E&=\sum_{n=4}^7 n\cdot 2 \cdot {n-1\choose 3}\left(\frac{1}{2}\right)^n =\frac{93}{16}\\ &=5.8125. \end{align}$

This is a modification of problem 1981-4 from the A Friendly Mathematics Competition by Rick Gillman (ed.)

Marcos Carreira created the Markov chain in Solution 2 and ran Mathematica to produce the illustrations and find the answer. Solution 3 is by Amit Itagi.