Waiting for Multiple Heads
Problem

$n=3$
For the first appearance of three of heads in $n$ tosses,
- the last one needs to be a heads,
- the total number of heads needs to be $3$ (in the limit the rare event of no heads will play no role),
- the first two heads could be in any of the first $n-1$ tosses.
Thus we get the expectation of the first occurrence of three heads:
$\displaystyle E_3(p)=\sum_{n=3}^{\infty}n\frac{(n-1)(n-2)}{2!}(1-p)^{n-3}p^3=\frac{3}{p}.$
To see that, introduce $\displaystyle f(x)=\sum_{n=3}^{\infty}n\frac{(n-1)(n-2)}{2!}x^{n-3}.$ Integrate three times from $0$ to $x$ to get $\displaystyle \sum_{n=3}x^n=\frac{x^3}{1-x}.$ Differentiate three times to find $\displaystyle f(x)=\frac{3}{(1-x)^4}.$ Then substitute $x=1-p$ and multiply by $\displaystyle \frac{p^3}{2!}$
$n=4$
For the first appearance of four of heads in $n$ tosses,
- the last one needs to be a heads,
- the total number of heads needs to be $4$ (in the limit the rare event of no heads will play no role),
- the first three heads could be in any of the first $n-1$ tosses.
Thus we get the expectation of the first occurrence of four heads:
$\displaystyle E_4(p)=\sum_{n=4}^{\infty}n\frac{(n-1)(n-2)(n-3)}{3!}(1-p)^{n-4}p^4=\frac{4}{p}.$
Follow the steps described above but with four integrations followed by four differentiations.
Markov Chain
It seems reasonable to conjecture that on average one will need to wait $\displaystyle \frac{N}{p}$ flips before getting $N$ heads the first time. I'll describe a process of obtaining this result for $N=5$ that will make the assertion obvious. The process is based on constructing the Markov chain that describe flipping a coin and counting the number of heads.
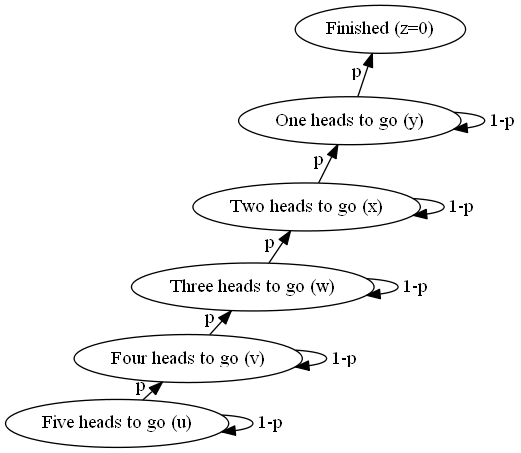
There are six nodes, corresponding to the number of heads from $0$ to $5.$ The one at the bottom corresponds to a zero count of heads. This is, say, state $1.$ We move from one state to the next with the probability of $p$ and stay in the same state with the probability of $1-p.$
There are six variables $u,$ $v,$ $w,$ $x,$ $y,$ $z,$ corresponding to the average number of coin flips that yet required to get to the last state of having five heads. These six variables are connected as in the following system:
$\left\{\begin{align} &z=0\\ &y=1+(1-p)y+pz\\ &x=1+(1-p)x+py\\ &w=1+(1-p)w+px\\ &v=1+(1-p)v+pw\\ &u=1+(1-p)u+pv. \end{align}\right.$
The free coefficient $1$ tells us that the count of heads changes with every transition from state to state. The system can be rewritten:
$\left\{\begin{align} &py=1\\ &px=1+py\\ &pw=1+px\\ &pv=1+pw\\ &pu=1+pv. \end{align}\right.$
A step-by-step substitution from the top down shows that $py=1,$ $px=2,$ $pw=3,$ $pv=4,$ $pu=5.$ The first four confirm our previous derivations; the last one confirms the conjecture, $\displaystyle E_5(p)=u=\frac{5}{p}.$ The way it was obtained shows how the general conjecture can be proved by induction.
Mathematica code
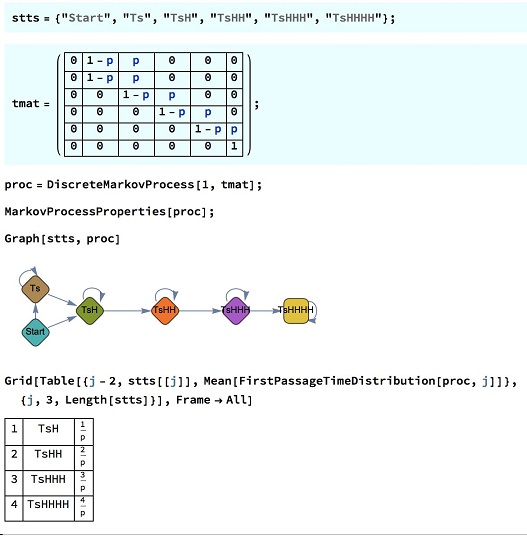
Monte Carlo verification

Mathematica code II, First run

Extra solution
Let $q=1-p$. Suppose we get $k$ heads for the first time after $n$ flips, then the first $n-1$ flips should have exactly $k-1$ heads and the last flip has to result in heads. The probability of this happening is
$Z(n,k)=C(n-1,k-1)p^kq^{n-k}.$
Thus, the expected number of flips before getting $k$ heads (assuming $k>0)$ is
$\displaystyle \begin{align} f(k)&=\sum_{n=0}^\infty nZ(n,k)=\sum_{n=0}^\infty nC(n-1,k-1)p^kq^{n-k} \\ &=\sum_{n=0}^\infty n\left[\frac{k}{n}C(n,k)\right]p^kq^{n-k}\\ &=kp^k\sum_{n=0}^\infty C(n,k)q^{n-k} \\ &=\frac{kp^k}{k!}\sum_{n=0}^\infty n(n-1)\ldots (n-k+1)q^{n-k}\\ &=\frac{p^k}{(k-1)!}\frac{\partial^k}{\partial q^k}\sum_{n=0}^\infty q^n \\ &=\frac{p^k}{(k-1)!}\frac{\partial^k}{\partial q^k}\frac{1}{1-q}. \\ f(3)&=\frac{p^3}{2!}\frac{\partial^3}{\partial q^3}\frac{1}{1-q}\\ &=\frac{p^3}{2!}\frac{3!}{(1-q)^4}=\frac{3}{p}. \\ f(4)&=\frac{p^4}{3!}\frac{\partial^4}{\partial q^4}\frac{1}{1-q}\\ &=\frac{p^4}{3!}\frac{4!}{(1-q)^5}=\frac{4}{p}. \end{align}$
Mathematica code II, Second run
Generalization of a problem: Flipping a coin, with probability of heads $p$, $0\lt p\lt 1$, what is the expected number of flips before getting $3, 4, m$ heads?
Nonconsecutive heads
Three nonconsecutive heads
We denote by $x$ an event we don't count and $H$ the heads on the coin.
$\begin{array}{ccccc} & \text{x} & \text{xH} & \text{xHxH} & \text{xHxHxH} \\ \text{x} & 1-p & p & 0 & 0 \\ \text{xH} & 0 & 1-p & p & 0 \\ \text{xHxH} & 0 & 0 & 1-p & p \\ \text{xHxHxH} & 0 & 0 & 0 & 1 \\ \end{array}$
with transition matrix
$ \pi=\left( \begin{array}{cccc} 1-p & p & 0 & 0 \\ 0 & 1-p & p & 0 \\ 0 & 0 & 1-p & p \\ 0 & 0 & 0 & 1 \\ \end{array} \right)$
We denote the dot product of the matrix $\pi^n= \underbrace{\pi.\pi\ldots \pi}_{n}$.
$\displaystyle\small{\begin{align} \pi^n=\left( \begin{array}{cccc} (1-p)^n & n (1-p)^{n-1} p & \frac{1}{2} (n-1) n (1-p)^{n-2} p^2 & 1-\frac{1}{2} (1-p)^{n-2} ((n-2) p ((n-1) p+2)+2) \\ 0 & (1-p)^n & n (1-p)^{n-1} p & (-n p+p-1) (1-p)^{n-1}+1 \\ 0 & 0 & (1-p)^n & 1-(1-p)^n \\ 0 & 0 & 0 & 1 \\ \end{array} \right)\end{align}}$
We have the transition probability from the initial state $S_0=x$ to $S_n=xHxHxH$ in $n$ throws
$\displaystyle p(S_n|S_0)=1-\frac{1}{2} (1-p)^{n-2} ((n-2) p ((n-1) p+2)+2)$
Hence we can derive the probability mass function pmf of the stopping (first passage) time distribution (indexed for 3 heads):
$\displaystyle \phi_{3,n}=p(S_{n-1}|S_0)-p(S_n|S_0)= \frac{1}{2} (n-2) (n-1) p^3 (1-p)^{n-3},\; n\geq 3 $
And the expected stopping time:
$\sum _{n=3}^{\infty } n \phi_n=\frac{3}{p}$
Four and more nonconsecutive heads
$\pi_4=\left( \begin{array}{ccccc} 1-p & p & 0 & 0 & 0 \\ 0 & 1-p & p & 0 & 0 \\ 0 & 0 & 1-p & p & 0 \\ 0 & 0 & 0 & 1-p & p \\ 0 & 0 & 0 & 0 & 1 \\ \end{array}\right)$
and $\displaystyle \phi_{4,n}= \frac{1}{6} (n-3) (n-2) (n-1) p^4 (1-p)^{n-4}.$ And the expected stopping time:
$\displaystyle \sum _{n=4}^{\infty } n \phi_{4,n}=\frac{4}{p}$
Generalizing, for $m$ heads,
$\displaystyle \phi_{m,n}= \frac{1}{m!} (n-m) (n-m-1) \ldots (n-3) (n-2) (n-1) p^m (1-p)^{n-m}$ or, more compactly, using the Pochhammer symbol for the rising factorial:
$\displaystyle \phi_{m,n}= \frac{1}{m!} (n-m)_m p^m (1-p)^{n-m}$
Finalmente
$\displaystyle \sum _{n=m}^{\infty } n \phi_{m,n}=\frac{m}{p}$
Consecutive Heads
Three consecutive heads
$\begin{array}{ccccc} & \text{x} & \text{H} & \text{HH} & \text{HHH} \\ \text{x} & 1-p & p & 0 & 0 \\ \text{H} & 1-p & 0 & p & 0 \\ \text{HH} & 1-p & 0 & 0 & p \\ \text{HHH} & 0 & 0 & 0 & 1 \\ \end{array}$
The matrix and the pmf of the first passage time distribution are unwieldy but we get for the expected stopping time
$\displaystyle \frac{1}{p^3}+\frac{1}{p^2}+\frac{1}{p}.$
Generalization
For $m$ consecutive heads:
$\displaystyle \sum_{i=1}^m\frac{1}{p^m}$
Remark
As a matter of fact, this is known as negative binomial distribution. To compute the expectation for $n$ heads just repeat the experiment "flips until $1$ head" $n$ times, so the expectation is linear in $n.$ https://en.wikipedia.org/wiki/Negative_binomial_distribution.
Acknowledgment
This problem is a natural extension of the previous one (with $n=2.)$ I am grateful to Josh Jordan for bringing up the topic of Markov chains and suggesting software from graphviz.org for their depiction. Marcos Carreira supplied the Mathematica code and the Monte Carlo verification for $n=3.$ N. N. Taleb used Mathematica in a somewhat different manner and this on two occasions. Extra solution is by Amit Itagi. The Remark is due to Long Huynh Huu.
|Contact| |Front page| |Contents| |Probability|
Copyright © 1996-2018 Alexander Bogomolny73579840
