A Problem of Two Liars

Both $A$ and $B$ tell the truth in one of three cases and lie in two of three cases. The three cases for $A$ and $B$ can be visualized as a $3\times 3$ square.

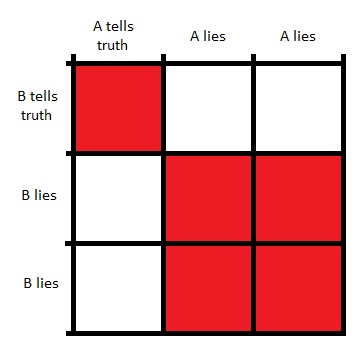
$B$ could claim that $A$'s statement is true if both were telling the truth or both lied. There are five red squares that correspond to these conditions. In only one of these (the upper left corner) $A$ was actually telling the truth. This happens in one of five cases, i.e., with the probability of $\displaystyle \frac{1}{5}.$

Let $E$ be the event that $A$ makes a statment and $B$ confirms. This can happen in two ways:

• $T:$ both $A$ and $B$ are telling the truth;
• $L:$ both $A$ and $B$ are lying.

$\displaystyle P(E)=P(T)+P(L)=\frac{1}{3}\cdot\frac{1}{3}+\frac{2}{3}\cdot\frac{2}{3}=\frac{5}{9}.$

Given that we observe $E,$ we are interested in finding the probability that the underlying process is, in fact, $T$ that is, $P(T|E).$ From the formula for conditional probabilities, $\displaystyle P(T|E)=\frac{P(T\cap E)}{P(E)}$ and $P(T\cap E)=P(T)$ because $T\subset E.$ In conclusion,

$\displaystyle P(T|E)=\frac{P(T)}{P(E)}=\frac{1/9}{5/9}=\frac{1}{5}.$

This is a paraphrase of problem 2.4.9 from R. Falk's Understanding Probability and Statistics (A K Peters, 1993).

Solution 2 is by Christian Adib.