A Three Group Split

Let's represent the three group split by three numbers "###," each standing for the amount of even numbers in a group. The order of the groups is of no consequence. $000$ is the starting configuration. There are nine open slots to place the first even number in. However it is done, the next state is $100.$

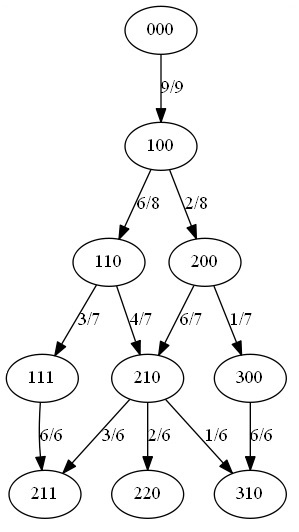
With one even number in place, there are $8$ slots - two in the same group as the first even number. Placing the second even number there moves to the state $200,$ otherwise, with probability $\displaystyle \frac{6}{8},$ will move to the state $110.$ We continue in this manner, distributing even numbers of which there are four.

When all is said and done, there are only three possible states with four even numbers: $211,$ meaning no group having three odd numbers, $220,$ and $310$ - in both cases there is one group (corresponding to $0)$ in which all numbers are odd.

The probability if getting into the state $220$ is

$\displaystyle\begin{align}P(220)&=\left(\frac{6}{8}\cdot\frac{4}{7}+\frac{2}{8}\cdot\frac{6}{7}\right)\cdot\frac{2}{6}\\ &=\frac{24+12}{56}\cdot\frac{1}{3}=\frac{3}{14}. \end{align}$

The probability if getting into the state $310$ is

$\displaystyle\begin{align}P(310)&=\frac{2}{8}\cdot\left(\frac{1}{7}\cdot\frac{6}{6}+\frac{6}{7}\cdot\frac{1}{6}\right)+\frac{6}{8}\cdot\frac{4}{7}\cdot\frac{1}{6}\\ &=\frac{1}{4}\cdot\frac{6+6}{42}+\frac{1}{14}=\frac{2}{14}. \end{align}$

Thus the probability of having a group of odd numbers is $\displaystyle \frac{2}{14}+\frac{3}{14}=\frac{5}{14}.$

This is a rephrase of a problem from the mathpages website by Kevin Brown.