Six Numbers, Three Inequalities

The answers to the questions are $\displaystyle \frac{1}{24}$ and $\displaystyle \frac{5}{24},$ respectively.

For the first problem, we choose four digits to place next to the inequality signs. These can be permuted in $4!=24$ ways of which only one satisfies all three inequalities. We conclude that the probability of this happening is $\displaystyle \frac{1}{24}.$

We can do a more complete counting: there are $\displaystyle {6\choose 4}=\frac{6!}{2!4!}$ to choose four numbers out of six, the other two can be permuted in $2!=2$ ways. Thus the sought probability is $\displaystyle \frac{6!2!}{2!4!6!}=\frac{1}{4!},$ as before.

For the second problem, observe that if four numbers $u,v,w,x$ fit the inequalities in the first question, i.e., $u\lt v\lt w\lt x$ then

$u\lt w\gt v\lt x\\ u\lt x\gt v\lt w\\ v\lt w\gt u\lt x\\ v\lt x\gt u\lt w\\ w\lt x\gt u\lt v$

Thus to every solution of the first question there correspond five solutions to the second. It follows that the probability of a random sequence satisfying the inequalities in the second question is $\displaystyle \frac{5}{24}.$

We can establish several rules. Let's call a sequence of consecutive square cells whose inner (but not the two outer) sides carry a symbol of inequality a run.

Rule 1: The event of inequalities satisfied in one run are independent of the event of the inequalties being satisfied in any other run.

We call a run consistent, if its inequalities are all the same, either $\lt$ or $\gt.$

Rule 2: For a grid of $n$ cells, the probability of satisfying a consistent run of length $k$ is $\displaystyle \frac{1}{n\choose k}.$

... to be continued ...

Dr. Pasquale Cirillo made a suggesion to make inequality symbols sparser which would allow to compare multidigit numbers.

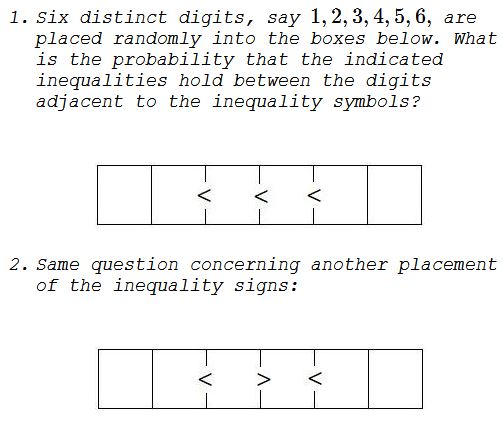
Practically it becomes a counting problem. Suppose there are $n-1$ inequality changes of $(x_1,x_2,\ldots,x_n)$.

Examples: suppose we have $a \lt b \gt c\lt d$, so $1$ rise followed by $1$ drop, then $1$ rise. We represent this by tuple $(1,1,1)$. If we have $a \gt b\lt c\lt d\lt e \gt f$, then this has representation $(1,3,1)$, i.e. one drop, $3$ raises, $1$ drop.

It does not matter if we start the sequence with a drop or a raise. Also, the counts for symmetric sequences is the same.

Denote the number of sequences for the tuple $(m_1,\ldots,m_q)$ as $a_{m_1,\ldots,m_q}.$ By the definition, $a_{m_1,\ldots,m_q}=a_{m_q,\ldots,m_1}$.

Some numbers: $a_{1}=1,a_{1,1}=2,a_{2}=1.$

$a_{1,1,1}=5,a_{1,2}=3,a_{3}=1,$ $a_{1,1,1,1}=16,$ $a_{1,1,2}=9,$ $a_{1,2,1}=11,$ $a_{1,3}=4,$ $a_{2,2}=6,$ $a_{4}=1.$

Note: $a_{1,1,1}=5$ and $a_{3}=1$ appeared in connection with the Twitter problem.

Recurrence relation: An example will show it, the general case is similar. Suppose we need to calculate $a_{2,3,2,1,2,1}$. We may assume we start with a rise. We have two valleys (convexities) between $3$ falls and $2$ raises and between $1$ fall and $2$ raises. What changes by the addition of last number when we drop once? This last number can be the lowest one, in which case all the others can freely move in $a_{2,3,2,1,2}$ ways.

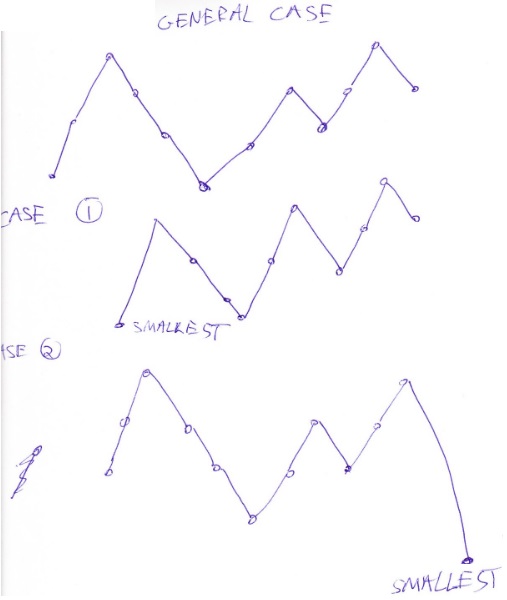
Or the lowest number can be the first and the others move freely in $a_{1,3,2,1,2,1}$ ways.

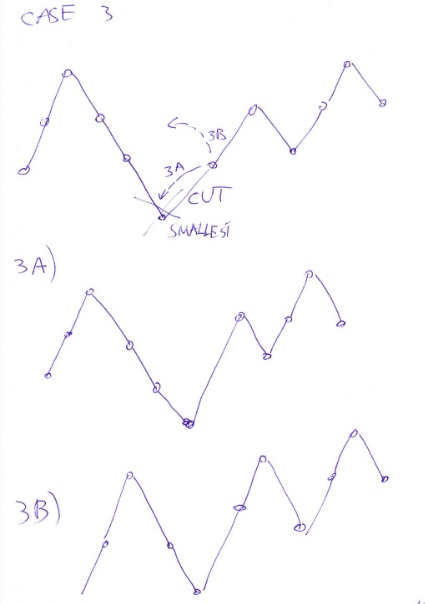
Or the lowest number can be in the first valley between $3$ and $2.$ In this case, we might have that the left neighbour is higher than right neighbour, in which case the counts are $a_{2,3,1,1,2,1}$ or the right neighbour is higher than the left neighbour, in which case the count is $a_{2,2,2,1,2,1}$.

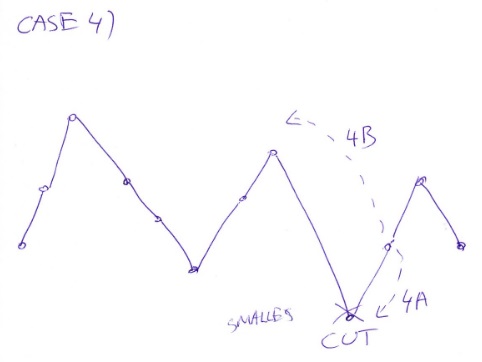
Similarly, in the second valley the counts are (depending which of the neighbours is higher) $a_{2,3,4,1}$ and $a_{2,3,2,1,1,1}$.

In conclusion

$\begin{align}a_{2,3,2,1,2,1}&=a_{1,3,2,1,2,1}+a_{2,3,2,1,2}+a_{2,3,1,1,2,1}\\ &\qquad\qquad+a_{2,2,2,1,2,1}+a_{2,3,4,1}+a_{2,3,2,1,1,1}\end{align}$

Examples:

$a_{1,1,1}=a_{1,1}+a_2+a_{1,1}\\ a_{2,2}=a_{2,1}+a_{1,2}\\ a_{2,1,1}=a_{1,1,1}+a_3+a_{2,1}\\ a_{1,1,1,1}=a_{1,1,1}+a_{1,1,1}+a_{2,1}+a_{2,1}\\ a_{1,1,1,2}=a_{1,1,1,1}+a_{1,1,2}+a_{2,2}+a_{1,3}\\ a_{1,1,1,1,1}=a_{1,1,1,1}+a_{2,1,1}+a_{1,2,1}+a_{1,2,1}+a_{1,1,1,1}$

These problems have been inspired by Donald Knuth's puzzles from the multi-author collection Puzzle Box, v 2.

Bogdan Lataianu is responsible for the Extra section.