Rolling a Die
Problem

Solution
There are six possible outcomes before the running total exceeds $12:$ $12,$ $11,$ $10,$ $9,$ $8,$ $7.$ Possible outcomes for any of these are listed below:
$\begin{array}{rccccccc} 12:&&13&14&15&16&17&18\\ 11:&&12&13&14&15&16&17\\ 10:&&11&12&13&14&15&16\\ 9:&&10&11&12&13&14&15\\ 8:&&9&10&11&12&13&14\\ 7:&&8&9&10&11&12&13\\ \end{array}$
$13$ appears as the most likely total as it's the only one with a chance to be reached in all six cases.
There are $36$ entries in the table with $13$ appearing $6$ times, $12$ and $14$ $5$ times, and so on. If we assign the probabilities to the possible totals according to the number of their occurrence in the table, we can get the expected value:
$\displaystyle\begin{align}E&=\frac{1}{36}[6\cdot 13+5(12+14)+4(11+15)+3(10+16)+2(9+17)+1(8+18)]\\ &=\frac{1}{36}\cdot 468=13. \end{align}$
Was this to be expected?
Simulation
Marcus Obendrauf ran the following simulation:
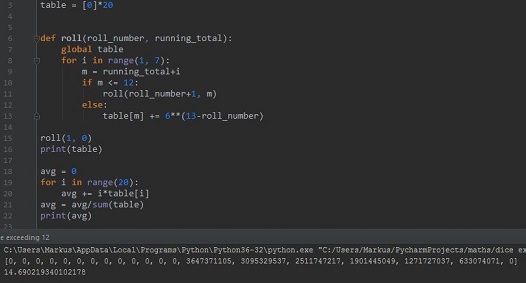
The simulation appears to confirm that $13$ as the most probable running total, but produces a different average, viz., $\approx 14.69.$ As a matter of fact, the penultimate totals of $7,$ $8,$ $9,$ $10,$ $11,$ $12$ have different probabilities of arriving at. This may question the logic of the above solution.
Acknowledgment
The problem came from Ross Honsberger's Mathematical Morsels, (MAA, 1978, #20). Honsberger credits C. C. Carter (Problem E771, AMM, 1848) as a proposer and N. J. Fine as a solver.
|Contact| |Front page| |Contents| |Probability|
Copyright © 1996-2018 Alexander Bogomolny73580587
