Waiting to Exceed 1
Problem
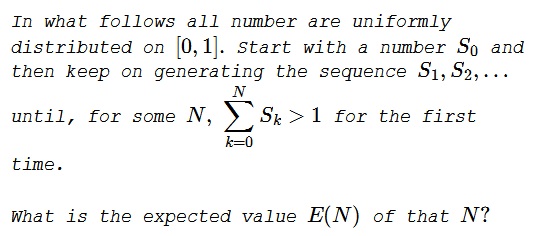
Solution 1

Solution 2
Let $T_n=\sum_{k=0}^n S_n$.
(1)
$P(T_n\lt 1)=\int_{S_0=0}^1\int_{S_1=0}^{1-T_0}\int_{S_2=0}^{1-T_1}\ldots\int_{S_n=0}^{1-T_{n-1}}dS_ndS_{n-1}\ldots dS_0.$
Let us make an observation here. For some natural numbers $k$ and $j$,
$\displaystyle \begin{align} \int_{S_k=0}^{1-T_{k-1}}\frac{(1-T_k)^j}{j!}dS_k &=\int_{S_k=0}^{1-T_{k-1}}\frac{(1-T_{k-1}-S_k)^j}{j!}dS_k \\ &=-\frac{(1-T_{k-1}-S_k)^{j+1}}{(j+1)!}\bigg\rvert_{0}^{1-T_{k-1}} =\frac{(1-T_{k-1})^{j+1}}{(j+1)!}. \end{align}$
Note, this result is also valid if $j=0$.
The integrand for the right-most integral in (1) can we written as $\displaystyle \frac{(1-T_n)^j}{j!}$ with $j=0$. Thus, the integrand keeps propagating through the integrals from right to left with $k$ decrementing by $1$ and $j$ incrementing by $1$ with every integral. Thus, we are left with
$\displaystyle P(T_n\lt 1) =\int_{S_0=0}^1 \frac{(1-T_0)^n}{n!} dS_0=\int_{S_0=0}^1 \frac{(1-S_0)^n}{n!} dS_0=\frac{1}{(n+1)!}.$
The desired expected value is
$\displaystyle \begin{align} &E(n) \\ &= \sum_{n=1}^\infty n\cdot P(T_{n-1}\lt 1\cap T_n\gt 1)=\sum_{n=1}^\infty n\cdot \left[P(T_n\gt 1)-P(T_{n-1}\gt 1\cap T_n\gt 1)\right] \\ &=\small{\sum_{n=1}^\infty n\cdot \left[P(T_n\gt 1)-P(T_{n-1}\gt 1)\right]=\sum_{n=1}^\infty n\cdot \left[\left(1-\frac{1}{(n+1)!}\right) -\left(1-\frac{1}{(n)!}\right)\right]}\\ &=\sum_{n=1}^\infty n\cdot \left[\frac{1}{n!}-\frac{1}{(n+1)!}\right] \\ &=1\cdot \left(\frac{1}{1!}-\frac{1}{2!}\right)+2\cdot \left(\frac{1}{2!}-\frac{1}{3!}\right)+\ldots=\frac{1}{1!}+(2-1)\cdot\frac{1}{2!}+(3-2)\cdot\frac{1}{3!}+\ldots \\ &=\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+\ldots=e-1\sim 1.72. \end{align}$
Solution 3
Let $T_n=\sum_{k=0}^nS_n$ and $N$ be the first value of $n$ for which $T_n\gt 1:$
$P(N\gt n)=P(T_0\lt 1,T_1\lt 1,\ldots,T_n\lt 1)=P(T_n\lt 1).$
It follows that
$\begin{align}P(N=n)&=P(N\gt n-1)-P(N\gt n)\\ &=P(T_{n-1}\lt 1)-P(T_n\lt 1). \end{align}$
We also know that $P(N=0)=0.$ Thus,
$\begin{align} E(N)&=\sum_{n=1}^{\infty}nP(N=n)=\sum_{n=1}^{\infty}n(P(T_{n-1}\lt 1)-P(T_n\lt 1))\\ &=\sum_{n=1}^{\infty}nP(T_{n-1}\lt 1)-\sum_{n=1}^{\infty}nP(T_n\lt 1))\\ &=\sum_{n=0}^{\infty}(n+1)P(T_{n}\lt 1)-\sum_{n=0}^{\infty}nP(T_n\lt 1))\\ &=\sum_{n=0}^{\infty}P(T_{n}\lt 1)\\ \end{align}$
Now, $P(T_0\lt 1)=P(S_0\lt 1)=1.$ By induction, $P(T_n\lt 1)=\displaystyle\frac{1}{(n+1)!},$ so that
$\displaystyle E(N)=\sum_{n=0}^{\infty}P(T_{n}\lt 1)=\sum_{n=0}^{\infty}\frac{1}{(n+1)!}=e-1.$
Remark
Note that above $T_n$ was defined as the sum of $n+1$ random variables. In a more common formulation, we would consider $T_n$ as the sum of $n$ random variables. In that case, the result would appear slightly different because then $P(T_n\lt 1)=\displaystyle\frac{1}{n!},$ so that we would have
$\displaystyle E(N)=\sum_{n=0}^{\infty}P(T_{n}\lt 1)=\sum_{n=0}^{\infty}\frac{1}{n!}=e.$
Solution 4
Call $E(x)$ the expected number of number selections for the sum to exceed $x.$ Since the first number is unformly distributed on $[0,1],$
$\displaystyle E(x)=1+\int_0^1E(x-t)dt.$
But $E=0$ for $x\lt 0,$ so if $0\le x\le 1$ this relation can be converted into
$\displaystyle E(x)=1+\int_0^xE(x-t)dt=1+\int_0^uE(u)du.$
It follows that $E'(x)=E(x),$ $E(0)=1,$ and so $E(x)=e^x.$ In particular, $E(1)=e.$
Acknowledgment
Solution 1 is by Marcos Carreira; Solution 2 is by Amit Itagi; Solution 3 is an adaptation from P. J. Nahin's Dueling Idiots and Other Probability Puzzles (Princeton University Press, 2000, 94-98); Solution 4 is an adaptation from D. Newman's A Problem Seminar (Springer-Verlag, 1982, problem 100).
|Contact| |Front page| |Contents| |Probability|
Copyright © 1996-2018 Alexander Bogomolny73578867
