Random Numbers And Obtuse Triangle

For $x,y,1$ to form a triangle at all, one needs the three inequalities:

$\begin{align} 1+x&\gt y,\\ 1+y&\gt x,\\ x+y&\gt 1. \end{align}$

The first two inequalities are satisfied automatically. Thus we should only consider the last one, $x+y\gt 1.$

The side of length $1,$ being the longest, the angle that lies opposite this side is the largest. It should not be acute or right, although the latter possibility has the probability of zero and can be disregarded.

The angle in question, say $\alpha$ is obtuse, $\cos\alpha\lt 0$ so that, from the Law of Cosines, $x^2+y^2\lt 1.$ Graphically, the point $(x,y)$ that satisfies $x+y\gt 1$ and $x^2+y^2\lt 1$ lies in the blue region, shown below:

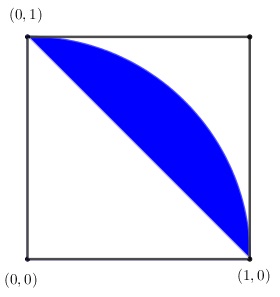
The sought probability is the area of that region:

$\displaystyle \frac{\pi}{4}-\frac{1}{2}=\frac{\pi-2}{4}.$

This problem is lifted from R. Honsberger's Ingenuity in Mathematics (MAA, 2012, Chapter 1).