Probability of No Distinct Positive Roots

The basis for the solution is naturally the quadratic formula: $\displaystyle x_{1,2}=\frac{-b\pm\sqrt{b^2-4c}}{2}.$

Now, it may be easier to determine when the equation does have distinct positive roots. This happens when

1. $c\gt 0,$
2. $b\lt 0,$
3. $b^2-4c\gt 0.$

With $b$ on the horizontal axis and $c$ on the vertical one, the blue points and only these satisfy the three conditions:

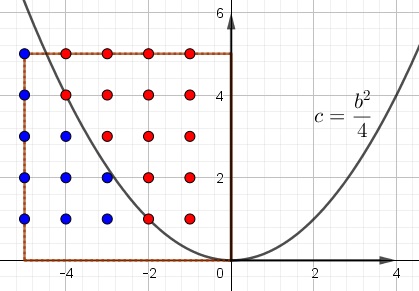
There are $10$ such points and $121=11^2$ ordered pairs that satisfy $|b|,C|\le 5,$ making the probability of distinct positive roots equal to $\displaystyle \frac{10}{121}.$ The probability of not having distinct positive roots is then $\displaystyle 1-\frac{10}{121}=\frac{111}{121}.$

This is problem 27 from the 1979 AHSME. This is a borrowing from The Contest Problem Book IV by R. A. Artino, A. M. Caglione and N. Shell (MAA, 1982).