Problem 25 from the Spring 2018 Mathcounts

The shape described by $0\le x,y,z\le 1$ and $x+y+z\le 1$ is a pyramid with a triangular base defined by three points $(0,0,0),$ $(0,1,0),$ and $(0,0,1)$ and the apex at $(0,0,1).$

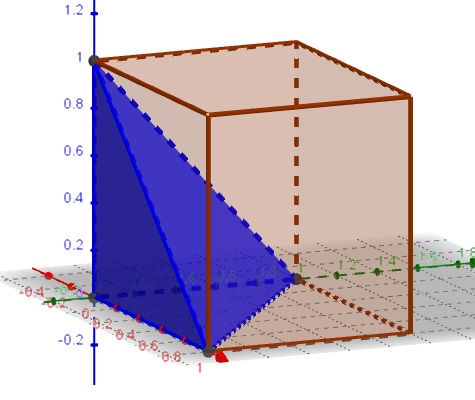
The volume of that pyramid is $\displaystyle \frac{1}{3}\cdot 1\cdot \left(\frac{1}{2}\cdot 1\cdot 1\right)=\frac{1}{6}.$ This is also the volume of the pyramid relative to that of the cube which is $1.$

The probability density function (pdf) of the unform distribution on $[0,1]$ is

$\displaystyle f(x)=\begin{cases} 1,&x\in[0,1]\\ 0,&elsewhere. \end{cases}$

Given two random variables, the pdf of their sum is the convolution of their pdf's. Same for three:

$\displaystyle\begin{align}g(z)&=\int_0^{\infty}f(z-y)\left(\int_0^{\infty}f(x)f(y-x)dx\right)dy\\ &=\begin{cases} \displaystyle \frac{z^2}{2},& 0\le z\le 1\\ \displaystyle \frac{1}{2}(-3+6z-2z^2),& 1\le z\le 2\\ \displaystyle \frac{1}{2}(9-6z+z^2),& 2\le z\le 3\\ \displaystyle 0,& elsewhere. \end{cases}\end{align}$

Due to the condition $x+y+z\le 1,$ we are only concerned with the distribution over $[0,1]$ such that the sought probability could be found from $\displaystyle \int_0^1\frac{z^2}{2}dz=\frac{1}{6}.$

I recast it as follows to help me visualize it better: For a lizard going up a wall, if it takes $3$ consecutive steps, each of which is a random value between $0$ and $1$ unit of length, what is the probability it will end up travelling less than $1$ unit of length?

The lizard's first step has a box car probability distribution function between $0$ and $1.$ For each of the value of its first step, you can add the second step. The second step by itself has a similar box car probability distribution function.

The sum of the first $2$ steps has a probability distribution function (PDF) that can be visualized by sliding the box car PDF of the second over the first and noting the overlapping area (increases linearly till $1$ and then decreases linearly till $2)$ {basically convolution}

The PDF of the sum of the $3$ steps can be visualized (again convolution) by sliding the box car PDF of the $3^{rd}$ step on the linear PDF of the sum of the first $2$ steps and noting how the overlap area evolves. Its area under $x^2/2$ for $0\lt x\lt 1.$ So it's $1/6.$

To elaborate the last part: The PDF for the sum of the $3$ steps (let call it $x$ for now) has a roughly bell shape between $0$ and $3,$ but is just $x^2/2$ in the range $0\lt x\lt 1.$ Thus, $P(x\lt 1)$ is the area under $x^2/2$ for $0\lt x\lt 1.$ So it's $1/6.$

Josh Jordan has kindly brought to our attention problem 25 from the Spring 2018 Mathcount competition.

Solution 2 is by N. N. Taleb; Solution 3 is by Thamizh Kudimagan.