Lucky Contest Winners

The simplest way to approach the problem is to consider the associated sample space. There are two girls and two boys from which a pair of winners is going to be drawn. Let's denote the girls $G$ and $g$ and the boys $B$ and $b.$ Formally speaking, there are $16 = 4\times 4$ possible ordered pairs formed by the four letters. However, from the context of the problem, the repetitions, like $GG,$ make no sense and should be excluded outright.

The three problems (with the last coming first) are collected in the tables below.

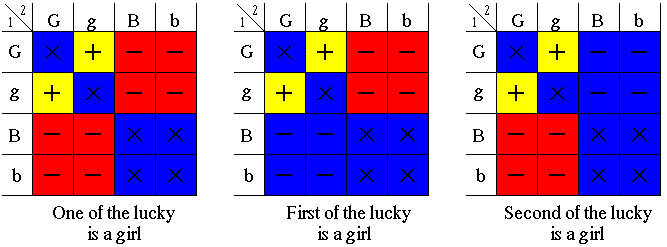
The legend is this: the impossible pairs (two boys or the same girl twice) are marked with a $'\times'.$ The two girl combinations are marked with $'+'$ and all the others with $'-'.$ In the first question (the middle table), the first member of the pair is known to be a girl, making the four combinations in the lower left corner impossible. These are also colored blue. A similar treatment applies to the upper right corner in the last table (second question.) Of the remaining squares the ones with favorable outcomes - $Gg$ or $gG$ - are colored yellow, the unfavorable ones red.

For the first two questions there are $6$ possible outcomes: $2$ favorable and $4$ unfavorable. In both cases then, the probability that two girls have been selected to advance to the national finals is $\displaystyle \frac{2}{6} = \frac{1}{3}.$

For the third question, you were as likely to cast your eyes on the first girl as on the second. By the Symmetry Principle, the probabilities of the two events are equal to $\displaystyle \frac{1}{2}$ whereas each of the girls had an individual probability of $\displaystyle \frac{1}{3}$ to be a winner. Thus the total probability of both girls is $\displaystyle \frac{1}{2}\cdot\frac{1}{3}+\frac{1}{2}\cdot\frac{1}{3}=\frac{1}{3}.$

For the fourth problem, there are $10$ possible outcomes, with only two favorable. The probability of having two lucky girls is then $\displaystyle \frac{2}{10} = \frac{1}{5}.$

1. If the girl that you saw on the stage was the first winner, then out of the three students left for the random drawing for a second winner, only one is a girl, and two are boys. The chances that the second one is also a girl will be $1$ in $3,$ or $\displaystyle \frac{1}{3}.$

   However, if the girl that you saw on stage was actually the second winner, then the chance that the first winner was also a girl is $\displaystyle \frac{1}{2},$ because before the first girl was picked, there were two girls and two boys, so the chance of a choosing a girl was then $2$ in $4,$ or $\displaystyle \frac{1}{2}.$

2. (Same as above) If the girl that you saw on the stage was the first winner, then out of the three remaining students, one is a girl and two are boys, so the chances that the second winner will also be a girl is $\displaystyle \frac{1}{3}.$

   (Different than above) It doesn't make any difference whether you saw the first girl or the second girl; the fact that you saw a girl winning at all means that there is only a $1$ in $3$ chance that the other winner was a girl, so, the probability that the first winner was also a girl if the girl that you see on the stage is the second winner is also $\displaystyle \frac{1}{3}.$

Remark

The solutions are followed by an advice to run a simulation. Before you do, give a thought to the fact that the second part of the first solution does not exploit the fact that the fellow you saw as the second winner was a girl. The argument would be the same if you saw a boy. This should make one suspicious of this line of reasoning.

To strengthen the second (and mine) solution we may apply the Bayes' theorem. In our notations, we would like to evaluate $P(G|g)$ - the probability that the first winner was a girl provided the second winner was also a girl. We accept as known (obvious or from the argument above) that

• $\displaystyle P(G) = P(B) = \frac{1}{2},$ i.e., the probabilities of the first winner being a girl or a boy are both equal to $\displaystyle \frac{1}{2}.$

• $\displaystyle P(g|G) = \frac{1}{3},$ i.e., the probability of the second winner being a girl provided the first one was a girl is $\displaystyle \frac{1}{3}$ (Solutions 1 and 2).

• $\displaystyle P(g|B) = \frac{2}{3},$ i.e., the probability of the second winner being a girl provided the first one was a boy is $\displaystyle \frac{2}{3}.$ This is because when the first boy was out after the first drawing, there remain two girls and one boy for the second drawing.

Now let's use Bayes' formula:

$\displaystyle \begin{align} P(G|g)&= \frac{P(Gg)}{P(g)}=\frac{P(g|G)P(G)}{P(g|G)P(G) + P(g|B)P(B)}\\ &= \frac{\displaystyle \frac{1}{3}\cdot \frac{1}{2}}{\displaystyle \frac{1}{3}\cdot \frac{1}{2} + \frac{2}{3}\cdot \frac{1}{2}}= \frac{\displaystyle \frac{1}{3}}{\displaystyle \frac{1}{3} + \frac{2}{3}}\\ &= \frac{1}{3}. \end{align}$

Looking back, it might have been easier to evaluate $P(Gg)$ outright. This the probability that the two winners were both girls. There are $\displaystyle {4\choose 2} = 6$ cases to chose $2$ items out of four. We are only interested in one selection. Therefore, $\displaystyle P(Gg) = \frac{1}{6}.$ Divided by $P(g)$ which is $\displaystyle \frac{1}{2},$ we obtain $\displaystyle P(G|g) = \frac{1}{6} \div \frac{1}{2} = \frac{1}{3}.$

This is a remake of an old page. Years ago when Mike Shaughnessy became the NCTM president, he inaugurated a new section Problem to Ponder of their Newsletter. Years past, I can't locate the problem online. The problem consisted of two parts; I added the third and the fourth questions. The above solution to the third question is by Josh Jordan and Thamizh Kudimagan who also suggested the formulation of the fourth question.

Solution 3 appeared in the July 15, 2010 issue of the NCTM Newsletter.