Lights on a Christmas Tree
Problem

Solution
The state of a light depends on the number of factors of the corresponding number. All integers but squares have en even number of distinct factors. For every factor, a light was switched on/off. After an even number of such operations the light is in its original state - off.
The last light to which the algorithm applied was $\#100.$ At this point, the only lights that are on correspond to the squares between $1$ and $100,$ inclusive. There are ten of them. Thus the probability of a random light being on is $\displaystyle \frac{10}{100}=\frac{1}{10}.$
Illustration
A step-by-step the lights on/off state is well represented by the diagram below:
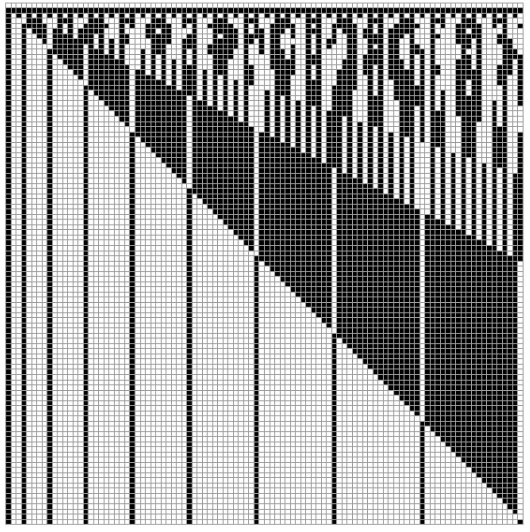
Acknowledgment
This is a paraphrase of problem 65277 from a Russian problem collection. The illustration is by Marcos Carreira.
|Contact| |Front page| |Contents| |Probability|
Copyright © 1996-2018 Alexander Bogomolny73579757
