Distributing Balls of Two Colors in Two Bags
Problem

Examples
Let $W_1,W_2$ stand for the number of white balls placed into two bags; similarly, $B_1,B_2.$ If $P(W)$ is the probability of drawing a white ball, we have several examples:
$\displaystyle \begin{array}{c|c|c|c|c} W_1&B_1&W_2&B_2&P(W)\\ \hline 5&5&5&5&\frac{1}{2}\cdot\frac{1}{2}+\frac{1}{2}\cdot\frac{1}{2}=\frac{1}{2}\\ 10&0&0&10&\frac{1}{2}\cdot 1+\frac{1}{2}\cdot 0=\frac{1}{2}\\ 3&7&7&3&\frac{1}{2}\cdot\frac{3}{10}+\frac{1}{2}\cdot\frac{7}{10}=\frac{1}{2}\\ 3&3&7&7&\frac{1}{2}\cdot\frac{1}{2}+\frac{1}{2}\cdot\frac{1}{2}=\frac{1}{2} \end{array}$
Solution
The best way is to set $W_1=1,$ $B_1=0,$ $W_2=9,$ $B_2=10.$ Then
$\displaystyle P(W)=\frac{1}{2}\cdot 1+\frac{1}{2}\cdot\frac{9}{19}=\frac{14}{19}\approx 0.7368$
Below is a graph of the function $\displaystyle f(x,y)=\frac{1}{2}\left(\frac{x}{x+y}+\frac{10-x}{20-x-y}\right)$ in the region $(0,10)\times (0,10).$
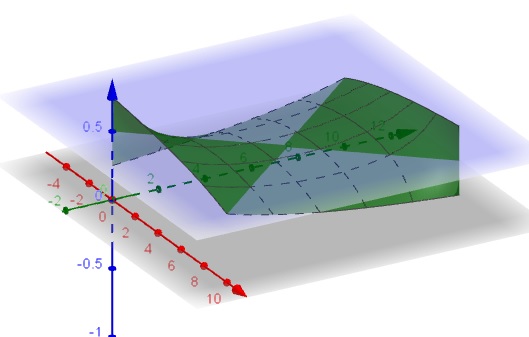
Here $x$ corresponds to $W_1,$ $y$ to $B_1,$ etc.
For integer values the maximum of $f$ is attained for $f(1,0)$ and $f(9,10)$ which are practically the same distribution.
The maximum probability could not exceed $75\%$ because there is always a bag where at most $50\%$ of balls are white and another where at most $100\%$ of balls are white.
Remark
In the diagram, the function $\displaystyle f(x,y)=\frac{1}{2}\left(\frac{x}{x+y}+\frac{10-x}{20-x-y}\right)$ appear to max out at the corners $(0,0)$ and $(10,10).$ This is probably due to software interpretation of one of the values $f(0,0),$ $f(10,10)$ as $\displaystyle \frac{1}{2},$ the other as $1.$ From the view point of probabilities, neither makes sense. Drawing a ball from an empty bag could not be assigned either $\displaystyle \frac{1}{2}$ or $1$ as a probability.
Acknowledgment
This is a paraphrase of problem 2.3.9 from R. Falk's Understanding Probability and Statistics (A K Peters, 1993).
Among other places on the web, the problem has been discussed in a thread started by John Baez, with a simple argument by Qiaochu Yuan, used above.
|Contact| |Front page| |Contents| |Probability|
Copyright © 1996-2018 Alexander Bogomolny73579850
