Inheriting Inequality
Problem
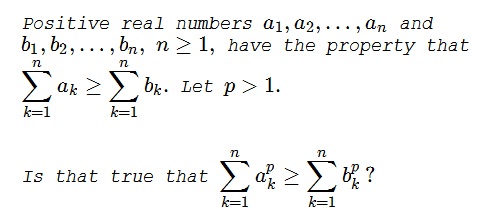
Solution
The answer is, Yes, and follows from Karamata's theorem. The sequences can be so rearranged as to satisfy Karamata's majorization requirement. Since the function $f(x)=x^p$ is convex and strictly increasing for $p\gt 1$ Karamata's theorem applies to establish $\displaystyle \sum_{k=1}^na_k^p\ge\sum_{k=1}^nb_k^p.$
Acknowledgment
The question arose following N.N. Taleb's similar inquiry with $p\lt 1.$
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73576744
