Expectation of Pairings
Problem
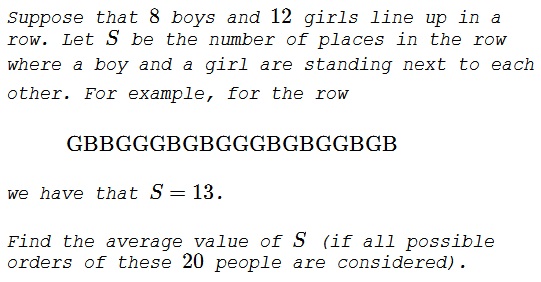
Solution 1
In general, let's consider a group of $m$ boys and $n$ girls. Let $P_k$ be the probability of having a couple boy/girl or girl/boy in positions $(k,k+1),$ $k=1,2,\ldots,m+n-1.$ From the point of view of chance all $P_k$ are the same, $P_k=P,$ $k=1,2,\ldots,m+n-1.$ Thus, similar to a problem of coin tossing, the expectation $E$ in question is $E=(m+n-1)P.$
To find $P,$ note that, once, a boy and a girl found themselves next to each other, the remaining boys and girls could be arranged in $\displaystyle {n+m-2\choose n-1}$ ways. This should be multiplied by $2$ because we do not distinguish the order in which the selected couple comes in the sequence. On the other hand, there are $\displaystyle {n+m\choose n}$ possible arrangements, implying
$\displaystyle P=\frac{\displaystyle 2 {n+m-2\choose n-1}}{\displaystyle {n+m\choose n}}=\frac{2nm}{(n+m)(n+m-1)}.$
We conclude that $\displaystyle E=(m+n-1)P=\frac{2nm}{n+m}.$ For $m=8$ and $n=12$ this gives $\displaystyle \frac{48}{5}.$
Solution 2
There are $\displaystyle \frac{m}{n+m}$ to choose a boy and $\displaystyle \frac{m}{n-m-1}$ to choose a girl from the remaining group. The probability of their being next to each other is $\displaystyle 2\cdot\frac{m}{n+m}\cdot\frac{m}{n-m-1}=\frac{2nm}{(n+m)(n+m-1)}.$ This could happen in $n-1$ positions, making the expectation equal
$\displaystyle E=(n+m-1)\cdot\frac{2nm}{(n+m)(n+m-1)}=\frac{2nm}{n+m},$
the harmonic mean of $m$ and $n.$
Acknowledgment
This problem is a slight modification of problem #30 from the 1989 AHSME. The problem from AHSME was reproduced in 102 Combinatorial Problems by T. Andreescu, Z. Feng (Birkhäuser, 2003, #22).
|Contact| |Front page| |Contents| |Probability|
Copyright © 1996-2018 Alexander Bogomolny73515774
