Concerning Even Number of Heads
Problem

Solution 1
Let $P(n)$ be the probability of having an even number of heads after $n$ coin tosses. Obvioiusly, $P(0)=1,$ as $0$ is an even number. Also, $1-P(n)$ is the probability of having an odd nunber of heads after $n$ tosses.
If the number of heads was even after $n$ tosses, it will remain even next time with probability $1-p;$ if the number of heads was odd it will become even with probabiliy $p.$ Thus, we can establish that $P(n)$ satisfies the following recurrence relation:
$P(n+1) = p(1-P(n))+(1-p)P(n)=p+(1-2p)P(n),$
with the intial condition $P(0)=1.$ To make sure that we are on a right treck, $P(1)=p+(1-2p)P(0)=1-p,$ the probability of having a tails and, in this case, keeping the number of heads even. To solve the recurrence, assume $P(n)=A+Ba^n,$ for some constants $A,$ $B,$ and $a:$
$A+Ba^{n+1}=p+(1-2p)(A+Ba^n).$
Handling the expressions by $A$ and $B$ separately gives
$\begin{align} &A=p+(1-2p)A\\ &Ba^{n+1}=(1-2p)Ba^n. \end{align}$
We find $\displaystyle A=\frac{1}{2},$ independent of $p,$ and $B$ arbitrary, provided $a=1-2p.$ Thus the solution to the recurrence relation appears to be
$\displaystyle P(n)=\frac{1}{2}+B(1-2p)^n.$
To detemine $B,$ we'll use the initial condition: $\displaystyle 1=P(0)=\frac{1}{2}+B,$ which gives $\displaystyle B=\frac{1}{2},$ with the finalform of the solution $\displaystyle P(n)=\frac{1}{2}+\frac{1}{2}(1-2p)^n.$
For a fair coin, i.e., if $\displaystyle p=\frac{1}{2},$ $\displaystyle P(n)=\frac{1}{2},$ independent of $n.$
To answer the second question, for the first appearance of an even number of heads in $n$ tosses,
- the last one needs to be a heads,
- the total number of heads needs to be $2$ (in the limit the rare event of no heads will play no role),
- the first heads could be in any of the first $n-1$ tosses.
Thus we get the expectation of the first occurence of an even number of heads:
$\displaystyle E(p)=\sum_{n=2}^{\infty}n(n-1)(1-p)^{n-2}p^2=\frac{2}{p}.$
(Denote, say, $\displaystyle f(x)=\sum_{n=2}^{\infty}n(n-1)x^{n-2}.$ Integrate twice from $0$ to $x$ to get $\displaystyle \sum_{n=2}x^n=\frac{x^2}{1-x}.$ Differentiate twice to find $\displaystyle f(x)=\frac{2}{(1-x)^3}.$ Then substitute $x=1-p$ and multiply by $p^2$ that was left over.)
Thus, $\displaystyle E\left(\frac{1}{4}\right)=8,$ $\displaystyle E\left(\frac{1}{2}\right)=4,$ $\displaystyle E\left(\frac{3}{4}\right)=\frac{8}{3}.$
Solution 2
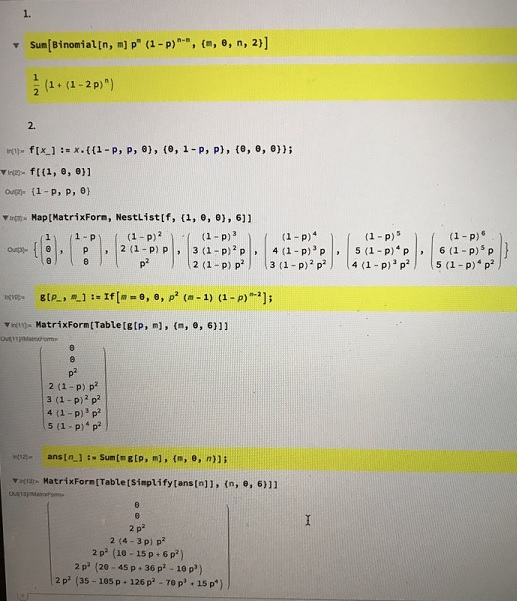
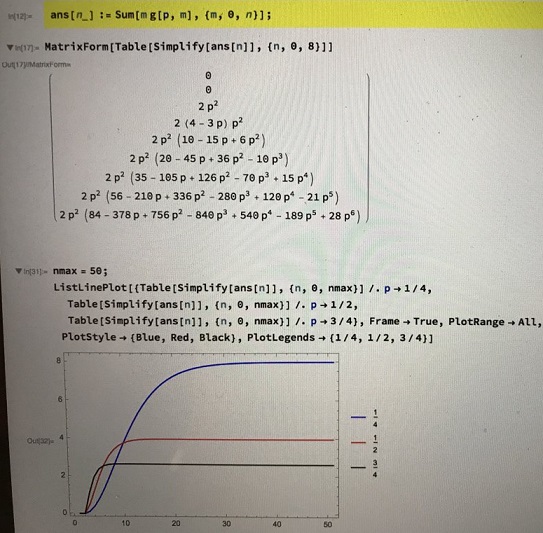
Acknowledgment
This is an extension of a problem from Paul J. Nahin's Will You Be Alive 10 Years From Now? Solution 2 is by Marcos Carreira.
|Contact| |Front page| |Contents| |Probability|
Copyright © 1996-2018 Alexander Bogomolny73561609
