Probability of Equilateral Triangle
Problem
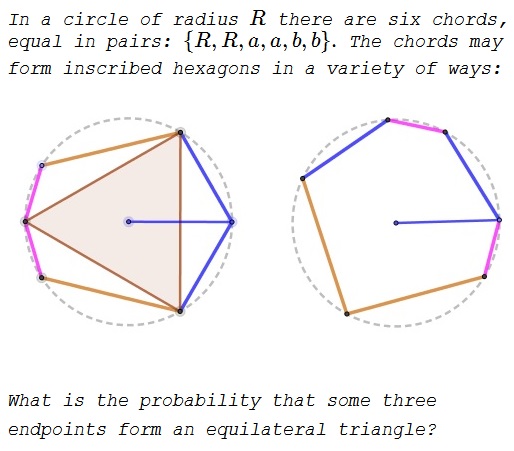
Solution
Let $\Phi(x)$ be the angle subtended by a chord of length $x$ at the center. $\Phi(R)=60^{\circ}$. Let us work under the assumption that $a\neq R$. This also implies that $a\neq b$, for if $a=b$, then the only way $\Phi(R)+\Phi(a)+\Phi(b)=180^{\circ}$ is if $a=b=R$. WLOG, let $a\lt R\lt b$ (One of $a$ and $b$ has to be smaller than $R$ and the other greater than $R$ because $\Phi(a)+\Phi(b)=120^{\circ}).$ Let $\Phi(a)=\alpha$ and $\Phi(b)=120^{\circ}-\alpha.$ The only additive combinations of the $\Phi's$ that result in $120^{\circ}$ are $2\Phi(R)$ and $\Phi(a)+\Phi(b).$ Thus, the allowed permutations of $\{R,R,a,a,b,b\}$ to get us the equilateral triangle are the permutations of $(R,R,a,b,a,b)$ where permutations are allowed within each of the two $(a,b)$ units and the entire set can be permuted in a cyclic manner.
The total number of permutations of the set are
$\displaystyle P_{tot}=\frac{6!}{2\times 2\times 2}=90,$
with each $2$ in the denominator discounting the permutations within the same kind of chords. The number of valid permutations of the kind $(R,R,...)$ are $2\times 2=4$ ($2$ permutations within each $(a,b)$ unit). $6$ cyclic permutations can be generated from each of the $4$ permutations. Thus $P_{valid}=4\times 6=24$. Hence, the required probability is
$\displaystyle Prob=\frac{P_{valid}}{P_{tot}}=\frac{24}{90}=\frac{4}{15}\sim 0.267.$
Acknowledgment
The problem has been inspired by a question from Thanos Kalogerakis. The above solution is by Amit Itagi.
|Contact| |Front page| |Contents| |Probability|
Copyright © 1996-2018 Alexander Bogomolny73578828
