Outline Mathematics
Geometry

Three Congruent Rectangles

A geometry problem that requires a little logic and algebra:

 

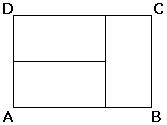
Reactangle ABCD contains three small congruent rectangles. If the smaller dimension of one of the small rectangles is 5 units, what is the area of rectangle ABCD in square units?

Solution


|Up| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

Solution

 

Reactangle ABCD contains three small congruent rectangles. If the smaller dimension of one of the small rectangles is 5 units, what is the area of rectangle ABCD in square units?

We may make three observations:

  1. Sides AD and BC,AD,AB,BC,CD of the big rectangle are equal.
  2. BC also serves as the big,big,small side of the small rectangle.
  3. (Looking at AD,) Two small sides of a small rectangle fit exactly in the small,big,small side of the big rectangle.

From #3, the small side of the big rectangle is twice,equal,twice,thrice the small side of the small rectangle, i.e., 10,5,10,20,30 units. From #2 (and #1), the big side of the small rectangle equals 10 units. The area of a rectangle equals the product of its sides. Therefore, the area of a small rectangle equals 5,5,10,20,30·10 = 50,50,60,70,80 square units. Three,Two,Three,Four small rectangles fit into the big one, making its area three times as large. It follows that the area of rectangle ABCD equals 3·50 = 150 unit².

Let's do this in a little more general way. Let x and y denote the small and the large dimensions of the small rectangle. This makes the area of the small rectangle xy,x + y,2x + y,3xy,xy and the area of the big rectangle 3xy. On the other hand, the small side of the big rectangle is 2x,x,2x,3x,4x whereas its big side measures x + y,x + y,2x + y,3xy,xy. It follows that the area of rectangle ABCD is also given by 2x·(x + y). The two quantities are equal:

  3xy = 2x·(x + y).

If x = 0, the problem degenerates into a case that requires no calculations. The big rectangles fills zero area as does a small rectangle. So assume x ≠ 0,0,1,2. This assumption allows us to divide both sides of the equation by x:

  3y = 2(x + y) = 2x + 2y,

which shows that

  y = 2x.

For x = 5, y = 10,5,10,20,30 and we are done.

References

  1. G. Lenchner, Math Olympiad Contest Problems For Elementary and Middle Schools, Glenwood Publications, NY, 1997

|Up| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

71082836