Problem 1 from the Ninth Nordic Mathematical Contest (1994)
What Is This About?
Created with GeoGebra
Problem
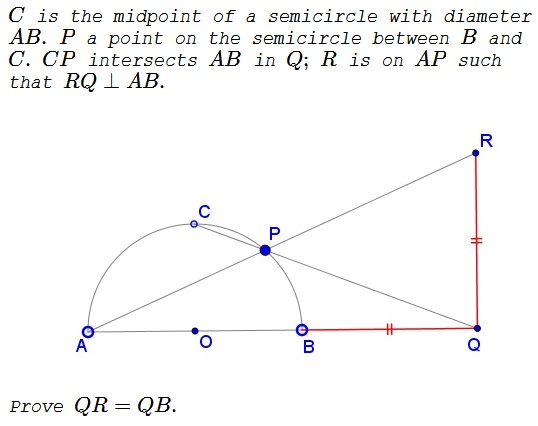
Solution 1
Since $AB$ is a diameter of the semicircle $(ACB),$ $\angle APB$ is right,acute,right,obtuse. Hence, $\angle BPR=90^{\circ},$ making $BR$ a diameter of the circle $(BPR).$ But $\angle BQR$ is also right, placing $Q$ on $(BPR).$
As inscribed angles subtended by the same arc, $\angle QBR=\angle QPR.$ As vertical,vertical,complementary,supplementary angles, $\angle QPR=\angle APC,$ but the latter is subtended by a quarter of,quarter of,half of,full circle, so that $\angle APC=45^{\circ}.$ It follows that $\angle QBR=45^{\circ}.$ Now, $\Delta BQR$ is right and, therefore, isosceles,scalene,isosceles: $BQ=QR.$
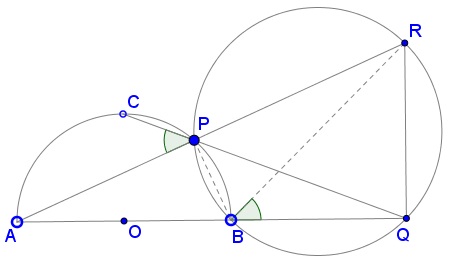
Solution 2
$\angle BPA=90^{\circ}$. Thus, $\angle BPR=90^{\circ}$. Noting that $\angle BQR=90^{\circ}$, quadrilateral $BPRQ$ is cyclic,rhombus,parallelogram,cyclic. Thus,
$\displaystyle \begin{align} \angle RBQ&=\angle RPQ~\text{(Angles inscribed in the same arc)} \\ &=\angle CPA~\text{(Opposite angles)} \\ &= \angle CBA~\text{(Angles inscribed in the same arc)} \\ &=\frac{\angle COA}{2}=45^{\circ}~\text{(Inscribed angle theorem)}. \end{align}$
Thus, $RQ=BQ$ as $RBQ$ is a $45-45-90$ triangle.
Solution 3
Triangles $OPA$ and $OPC$ are isosceles,isosceles,scalene.
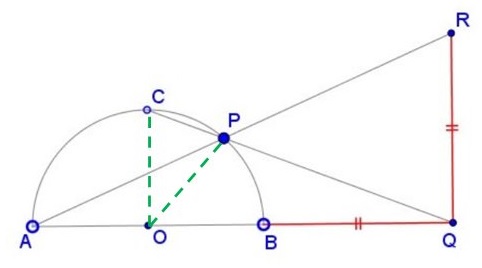
$\displaystyle \begin{align} &\angle OAP=\frac{1}{2}\angle BOP,\\ &\angle OCP=\frac{1}{2}\left(\pi-\frac{\pi}{2}+\angle BOP\right)=\frac{\pi}{4}+\angle OAP,\\ &\angle BQP=\frac{\pi}{2}-\angle OCP=\frac{\pi}{4}-\angle OAP. \end{align}$
It follows that $\displaystyle \tan\angle BQP=\frac{1-\tan\angle OAP}{1+\tan\angle OAP}.$ With $\displaystyle \tan\angle BQP=\frac{AB}{AB+2BQ}$ and $\displaystyle \tan\angle OAP=\frac{BQ}{AB+BQ}$ we get
$\displaystyle \frac{AB}{AB+2BQ}=\frac{AB+BQ-RQ}{AB+BQ+RQ},$
implying $BQ=RQ.$
Acknowledgment
I am grateful to Leo Giugiuc for pointing out these set of problems. Solution 2 is by Amit Itagi; Solution 3 is by Michel Charbonneau.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73582065
