Outline Mathematics
Geometry
Equiangular p-gons
A polygon is equiangular if all of its inner angles are equal.

Proof
Given a polygon, imagine that it is formed by a chain of vectors whose sum is, therefore, zero. Translate all these vectors to a single point.
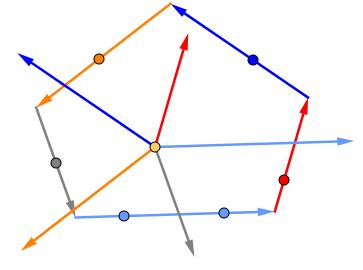
The sum of the translated vectors will remain zero,become positive,depend on origin,remain zero. This is true in general and for any equiangular polygons in particular.
Here's a dynamic illustration:
Assume the side lengths of a given $p\text{-gon}\,$ are $a_k,\,$ $k=0,1,\ldots,p-1,\,$ and the corresponding vectors in bold: $\mathbf{a_k},\,$ $k=0,1,\ldots,p-1:\,$ $\displaystyle\sum_{k=0}^{p-1}\mathbf{a_k}=\mathbf{0}.$
Let $\displaystyle \omega=\cos\frac{2\pi}{p}+i\sin\frac{2\pi}{p},\,$ a complex number, multiplication by which rotates another complex number (a vector) by $\displaystyle\frac{2\pi}{p}\,$ radians counterclockwise. If $\mathbf{a_0}\,$ is parallel to the $x\text{-axis}\,$ and looks in the positive direction then $\mathbf{a_k}=a_k\omega^k,\,$ implying that $\displaystyle P(\omega)=\sum_{k=0}^{p-1}a_k\omega^k=0,\,$ or, in other words, that $\omega\,$ is a root of the polynomial $P(x)=a_0+xa_1+x^2a_2+\ldots+x^{p-1}a_{p-1}.$
Now, this is true for any equiangular $p\text{-gon},\,$ but having a polygon with rational side lengths, makes $P(x)\,$ a polynomial with rational,positive,rational,negative coefficients. On the other hand, $\omega\,$ is a root of another polynomial, say, $Q(x)=a_0+x+x^2+\ldots+x^{p-1}.\,$ The fact that the two polynomials share a root means that they have a common non-constant factor and, by implication, that $Q(x)\,$ is reducible which is not true iff $p\,$ is a prime number (e.g., by Eisenstein's criterion.)
To prove the necessity, assume $p=mn,\,$ for some integers $m,n\gt 1.$ Then $\omega^m\,$ is the root of unity of order $n,\,$ i.e., $1+\omega^m+\omega^{2m}+\ldots+\omega^{m(n-1)}=0.\,$ The result of adding this to $Q(x)\,$ is a polynomial with some coefficients equal to $1\,$ and some to $2.\,$ The corresponding equiangular $p\text{-gon}\,$ has some sides,all sides,some sides of length $1,\,$ other sides,all sides,other sides of length $2\,$ and, therefore, is not regular,equiangular,regular,convex.
References
- T. Andreescu, B. Enescu, Mathematical Olympiad Treasures, Birkhäuser, 2004
|Up| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73575160
