Collinearity in Tangent Circles
What Is This About?
Created with GeoGebra
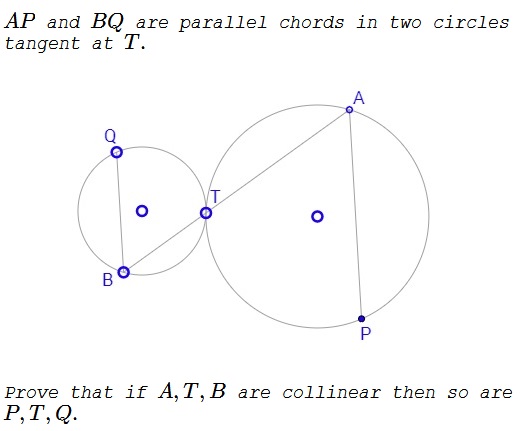
Problem
Solution
Assume that $A,T,B$ are collinear.
Since the two circle are tangent at $T,$ the line $XY$ tangent at $T$ to one is also tangent to the other.

If so, the vertical,exterior,interior,vertical,conjugate angles $ATX$ and $BTY$ are equal,equal,comparable. As is well known, the angle between a tangent and a chord is half,one third,half the angular measure of the arc cut off by the chords. It follows that the arcs $AT$ (opposite $P)$ and $BT$ (opposite $Q)$ are equal, implying that the inscribed,vertical,inscribed angles $APT$ and $BQT$ are equal.
In addition, since $AP\parallel BQ,$ $\angle PAT=\angle QBT.$ Thus we have two pairs of equal angles in triangles $APT$ and $BQT$ and may conclude that the third pair of angles are also equal: $\angle ATP=\angle BTQ,$ which only possible if the points $P,T,Q$ are collinear.
Acknowledgment
I am grateful to John Molokach for communicating to me the above problem from the Math: An Integral Part of Happiness facebook group.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73581351
