Outline Mathematics
Geometry
Angle in Right Triangle
Problem
In a right $\Delta ABC,$ points $D$ and $E$ divide the hypotenuse $AB$ into three equal parts.
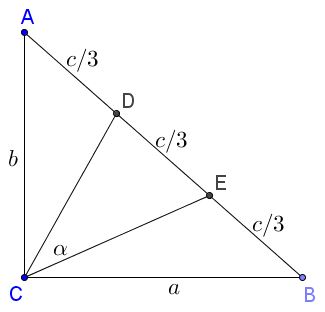
Assuming, $AB=c,$ $AC=b,$ $BC=a,$ $\alpha= \angle DCE,$ prove that $\tan\alpha=\displaystyle\frac{3ab}{2c^2}.$
Solution
Complete the triangle to rectangle $ACBF.$ Extend $CD$ to intersect $AF$ at $G;$ extend $CE$ to intersect $BF$ at $H.$
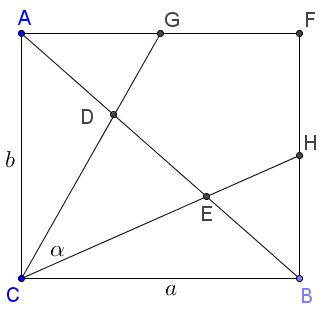
Conclude that $G$ is the midpoint,midpoint,endpoint of $AF;$ $H$ the midpoint of $BF.$ This follows from the similarity,similarity,equality,congruence of triangles $ADG$ and $BDC$ and that of $BEH$ and $AEC.$ (It is also nice to recollect an approach of dividing a segment into $n$ equal parts devised by two high school boys at the dawn of computer graphics software.)
We thus can immediately establish that
$\tan\angle ACG=\displaystyle\frac{a}{2b}$ and $\tan\angle BCH=\displaystyle\frac{b}{2a}.$
Since $\tan\alpha = \cot (90^{\circ}-\alpha),$ we get
$\begin{align}\displaystyle \tan\alpha &=\cot (\angle ACG+\angle BCH) \\ &= \frac{1-\tan(\angle ACG)\tan(\angle BCH)}{\tan(\angle ACG)+\tan(\angle ACG)} \\ &= \frac{1-1/4}{\frac{a}{2b}+\frac{b}{2a}} \\ &= \frac{3ab}{2(a^{2}+b^{2})} \\ &= \frac{3ab}{2c^{2}}, \end{align}$
by the Pythagorean theorem.
Acknowledgment
This is one of the problems from the book Jim Totten's Problems of the Week in memory of Jim Totten, a long time Problem Editor and later Editor-in-Chief of Crux Mathematicorum.
References
- J. G. McLoughlin et al, Jim Totten's Problems of the Week, World Scientific, 2013, #304
|Up| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73587425
