Outline Mathematics
Geometry

Angle Bisector in Square

What Is This About?

This is an adaptation of problem 1.3 (middle school) from the XIX (1997) Tournament of Towns.

Problem

Proof

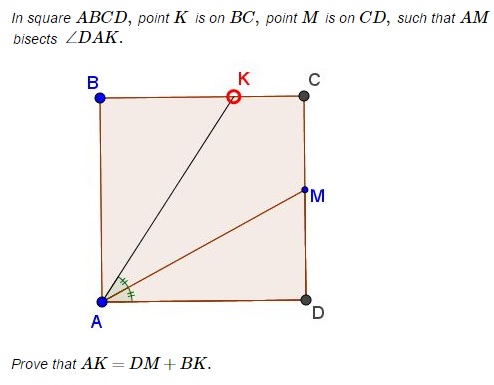
Proof 1

Rotate triangle $ADM\,$ around point $A\,$ 90^{\circ},$45^{\circ}$,$60^{\circ}$,$75^{\circ}$,$90^{\circ}$. The triangle will occupy position ABL,$MC$,$ACK$,$AKB$,$ABL$. Since angles $ADM\,$ and $ABL\,$ are right, $BL\,$ is a continuation of,a continuation of,perpendicular to $BC.$ It follows that $KL=BK+BL=BK+DM.$

Now, $\angle KAL=\angle KAB+$\angle BAL,$\angle BLA$,$\angle BAL$. On the other hand, $\angle BAL=\angle DAM=\angle MAK.\,$ Let's $\alpha\,$ denotes the latter. Then $\angle BAK=$90^{\circ}-2\alpha,$90^{\circ}-\alpha$,$90^{\circ}-2\alpha$,$90^{\circ}+2\alpha$,$90^{\circ}+\alpha$. It follows that

$\angle LAK=\angle BAL+\angle BAK=\alpha+(90^{\circ}-2\alpha)=90^{\circ}-\alpha=\angle ALB.$

This makes $\Delta AKL$ isosceles,isosceles,scalene, so that

$AK=BK+BL=BK+DM,$

as required.

Remark

Kunihiko Chikaya has pointed out that the same problem in a slightly different notations has been offered in 1987 at the entrace exams at Obihiro University of Agriculture and Veterinary Medicine.

References

1. L. E. Mednikov, A. V. Shapovalov, Toutnaments of Towns: World of Mathematics through Problems, MCNMO, 2016 (in Russian)

Proof 2

This proof is by Amit Itagi.

Let $\angle DAM=t\,$ and $AD=1.\,$ Then $\angle BAK=$90^{\circ}-2t,$90^{\circ}-t$,$90^{\circ}-2t$,$90^{\circ}+2t$,$90^{\circ}+t$. $DM=$\tan (t),$\sin (t)$,$\cos (t)$,$\tan (t)$,$\cot (t)$. $BK=\tan (90^{\circ}-2t)=$\cot (2t),$\sin (2t)$,$\cos (2t)$,$\tan (2t)$,$\cot (2t)$$=\displaystyle \frac{\cos (2t)}{\sin (2t)}.\,$ $AK=\displaystyle \frac{1}{\cos (90^{\circ}-2t)}=\frac{1}{\sin (2t)}.$

$\displaystyle \begin{align} DM+BK&=\frac{\sin (t)}{\cos (t)}+\frac{\cos (2t)}{\sin (2t)}\\ &=\frac{\cos (2t)\cos(t)+\sin(2t)\sin (t)}{\cos (t)\sin (2t)}\\ &=\frac{\cos (2t-t)}{\cos (t)\sin (2t)}\\ &=\frac{1}{\sin (2t)}=AK. \end{align}$

Proof 3

This proof is by Imad Zak.

Assume $AD=1,\,$ $\angle DAM=\alpha\,$ and $A=(0,0).\,$ Equation for $(AM)\,$ is $y=$x\tan\alpha,$x\tan\alpha$,$x\cot\alpha$,$x\cos\alpha$. At the intersection of $(CD)\,$ and $(AM)\,$ $x=1\,$ which gives $y=DM=$\tan (\alpha),$\sin (\alpha)$,$\cos (\alpha)$,$\tan (\alpha)$,$\cot (\alpha)$. The equation for $AK\,$ is $y=$x\tan 2\alpha,$x\tan 2\alpha$,$x\cot 2\alpha$,$x\cos 2\alpha$. For $y=1,\,$ $x=BK=$\displaystyle \frac{1-\tan^2\alpha}{2\tan\alpha},$\displaystyle \frac{1-\tan^2\alpha}{2\tan\alpha}$,$\displaystyle \frac{1-\cot^2\alpha}{2\cot\alpha}$,$\displaystyle \frac{1-\tan^2\alpha}{2\cot\alpha}$. Now,

$\displaystyle AK^2=AB^2+BK^2=1+\left(\frac{1-\tan^2\alpha}{2\tan\alpha}\right)^2=\left(\frac{1+\tan^2\alpha}{2\tan\alpha}\right)^2.$

Thus $AK=\displaystyle \frac{1+\tan^2\alpha}{2\tan\alpha}.\,$ Now verify

$\displaystyle DM+BK=\frac{1-\tan^2\alpha}{2\tan\alpha}+1=\frac{1+\tan^2\alpha}{2\tan\alpha}=AK.$

Important

Takis Chronopoulos has pointed out that the converse is also true:

If AM bisects $\angle DAK\,$ in rectangle $ABCD\,$ and $AK=DM+BK\,$ then $ABCD\,$ is a square,rhomb,isosceles trapezoid,square,cyclic.

Related material Read more...
	Basic Constructions
	Construction of the Angle Bisector
	Construction of the Perpendicular Bisector
	Existence of the Circumcenter

|Up| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny