Outline Mathematics
Geometry, Calculus
The Schwarz Lantern Explained
The Schwarz Lantern is in a sense a pathological shape that was described by the German mathematician Karl Hermann Amandus Schwarz (1843-1921) in 1880. The example demonstrates a difficulty in approximating a curved surface by planar polygons. A detailed description of the construction and an interactive illustration can be found elsewhere. Here I shall assume that we deal with a cylinder of height $1$ and a circular base of radius $1.$ The cylinder is cut into $M$ slices - rings, each of height $\displaystyle\frac{1}{M}.$ $N$ points are marked on circular rims of each slice, shifted in phase relative to each other half the distance between the points. Isosceles triangles are formed as shown below:

In each slice there are 2N,$N$,$2N$,$3N$ congruent isosceles triangles. Below I shall calculated the area of each of them and then, in order to find the area of the lantern, shall multiply the result by 2MN,$M$,$2N$,$2MN$.
One such (inverted) triangle ($ABC$) is depicted below. Its base $BC$ is a chord in the top circle $(O)$ of radius $1;$ its apex is at $A$, whereas $D$ is the midpoint of the base. Point $E$ is on the upper rim of the slice exactly above $A$ in the middle of the arc $BC.$
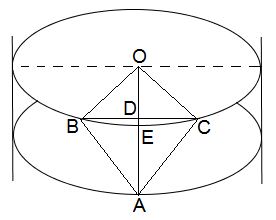
The area of $\Delta ABC$ equals $\displaystyle\frac{1}{2}AD\cdot BC,$ or, say, AD\cdot BD,$AE\cdot BC$,$AD\cdot BC$,$AD\cdot BD$.
In the right $\Delta BDO,$ $\displaystyle\angle BOD=\frac{1}{2}\frac{2\pi}{N}=\frac{\pi}{N},$ so that $BD=$\sin\displaystyle\frac{\pi}{N},$2\sin\displaystyle\frac{\pi}{N}$,$\sin\displaystyle\frac{\pi}{N}$,$\displaystyle\frac{1}{2}\sin\frac{\pi}{N}$. $OD$ will be need, too: $\displaystyle OD=\cos\frac{\pi}{N}.$ Next we need to find the altitude $AD.$ This will require a side view:
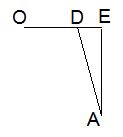
In $\Delta ADE,$ $\displaystyle AE=\frac{1}{M};$ $DE=1-\displaystyle\cos\frac{\pi}{N}=2\sin^{2}\frac{\pi}{2N},$ by one of the well-known formulas.
From the Pythagorean theorem, AD^{2}=DE^{2}+AE^{2},$AD^{2}=OE^{2}+AE^{2}$,$AD^{2}=DE^{2}+AE^{2}$, so that
$\displaystyle AD^{2}=DE^{2}+AE^{2}=4\sin^{4}\frac{\pi}{2N}+\frac{1}{M^2}\approx\frac{\pi^4}{4N^4}+\frac{1}{M^2},.$
because when $N$ is large $\displaystyle\frac{\pi}{2N}$ is small, and for small angles, say $\alpha,$ $\sin\alpha\approx$\alpha,$2\alpha$,$\alpha$,$\alpha /2$.
Putting everything together, the total area of the lantern is
$\displaystyle S=2MN\cdot AD\cdot BD\approx 2MN\cdot\frac{\pi}{N}\cdot\sqrt{\frac{\pi^4}{4N^4}+\frac{1}{M^2}}=2\pi\sqrt{\pi^{4}\frac{M^2}{4N^4}+1}.$
Now, the surface area of the cylinder equals $2\pi\cdot 1\cdot 1=2\pi.$ The approximate expression we found only tends to that value when $\displaystyle\frac{M^2}{N^4}\rightarrow 0.$ Which means that in order to approximate the surface of the cylinder, $M$ - the number of slice, and $N$ - the number of marked points on every rim, need to be chosen so that, as they grow, $\displaystyle\frac{M}{N^2}\rightarrow 0.$
Acknowledgement: This page was inspired by Mike Lawler's recent blog and Evelyn Lamb's earlier write-up.
|Up| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73571760
