Modern Vietnamese Classic
Problem
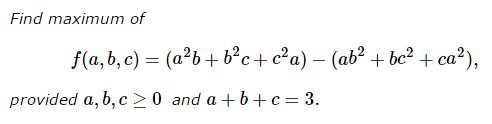
Solution 1
It is easily verified that $f(a,b,c)=(b-a)(a-c)(c-b).\;$ If $(b-a)(a-c)(c-b)\le 0,\;$ then $0\;$ is the obvious maximum. So assume $(b-a)(a-c)(c-b)\gt 0.\;$ WLOG, $b\gt c\gt a.\;$ Then $b=a+x\;$ and $c=a+y\;$ such that $x\gt y\gt 0.\;$ Further, $a+b+c=3\;$ becomes $x+y=3(1-a).$
Thus we have to find maximum of $g(x,y)=xy(x-y).\;$
Introduce $\displaystyle s=\frac{3(1-a)}{2}\;$ and $p=\sqrt{xy}.\;$ Obviously, $0\lt p\lt s\;$ and $x-y=2\sqrt{s^2-p^2}.$
Now, define, for every fixed $a\in [0,1),\;$ function $f_a:\;(0,s)\rightarrow\mathbb{R}\;$ with $f_a(p)=2p^2\sqrt{s^2-p^2}.$
As common, $\displaystyle f'_a(p)=2t\frac{2s^2-3p^2}{\sqrt{s^2-p^2}}\;$ so that
$\displaystyle \max f_a=f_a\left(s\sqrt{\frac{2}{3}}\right)=\frac{4s^3}{3\sqrt{3}}=\frac{3\sqrt{3}(1-a)^3}{2}.$
But $\displaystyle\frac{3\sqrt{3}(1-a)^3}{2}\le\frac{3\sqrt{3}}{2},\;$ implying that the sought maximum appears to be $\displaystyle \frac{3\sqrt{3}}{2}.\;$ This would be equivalent to the system
$\begin{cases} x+y &=3,\\ x-y &=\sqrt{3} \end{cases}$
such that $a=0,\;$ $\displaystyle b=\frac{3+\sqrt{3}}{2},\;$ $\displaystyle c=\frac{3-\sqrt{3}}{2}.$ Thus the maximum is indeed $\displaystyle \frac{3\sqrt{3}}{2}.\;$
Solution 2
We'll use Lagrange multipler technique with the constraint function $g(a,b,c)=a+b+c-3.\;$ As above, $f\;$ can be simplified to $f(a,b,c)=(a-b)(a-c)(b-c).\;$ Let $L(a,b,c,\lambda)=f(a,b,c)-\lambda g(a,b,c).\;$ Then
$\nabla_{\lambda,a,b,c}L=\left[\begin{array}{c} -a-b-c+3\\ 2ab-2ac-b^2+c^2-\lambda\\ a^2-2ab+2bc-c^2-\lambda\\ -a^2+2ac+b^2-2bc-\lambda \end{array}\right]$
Solving $\nabla_{\lambda,a,b,c}L=0\;$ gives the solution $\lambda=0,\;$ $a=b=c=1.\;$ Clearly, $f(1,1,1)\;$ is neither maximum nor minimum, for $\displaystyle f(3,0,0)\lt f(1,1,1)\lt f\left(2,\frac{3}{4},\frac{1}{4}\right).\;$ This means we need to look for maxima/minima at the boundary points of the constraint function $g(a,b,c).\;$ This is where eaither $a=0\;$ or $b=0,\;$ or $c=0.\;$ Now,
$\begin{align} f(0,b,c)&=b^2c-bc^2\\ f(a,0,c)&=ac^2-a^2c\\ f(a,b,0)&=a^2b-ab^2. \end{align}$
which are symmetric in $a,b,c.\;$ Choosing the first and maximizing as above with the constraint $b+c=3\;$ and $b\ge 0,\;$ $c\ge 0,\;$ we get
$\displaystyle f\left(0,\frac{1}{2}(\sqrt{3}-3)+3,\frac{1}{2}(3-\sqrt{3})\right)=\frac{3\sqrt{3}}{2}.$
Thus the maximum is $\displaystyle\frac{3\sqrt{3}}{2}.$
Solution 3
Let $T\,$ be the triangle with center $C=(1,1,1)\,$ given by $a+b+c = 3\,$ in the first octant of the $(a,b,c)-\text{space}.\,$ As
$f(a,b,c) = (a-b)(a-c)(b-c) = f(b,c,a) = -f(a,c,b),\,$
suffice it to look at $f\,$ in the sixth $S\,$ of $T\,$ given by $a \ge b \ge c.\,$ Let $P\,$ be a point of $S.\,$ If one moves on the line $CP\,$ away from $C,\,$ $f\,$ increases as each factor $(a-b),\,$ $(a-c),\,$ $(b-c)\,$ increases. The maximum of $f\,$ on $T\,$ lies therefore on the side of $S\,$ with $c=0,\,$ $a+b=3,\,$ $0\le a\le 3/2.\,$ The result follows at once by differentiating the cubic polynomial representing $f\,$ on this side.
Acknowledgment
The problem, along with the solution, has been posted by Leo Giugiuc at the CutTheKnotMath facebook page. Solution 1 is by Leo Giugiuc and Dan Sitaru; Solution 2 is by Uzair Baig; Solution 3 is by Grégore Nicollier.
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73574839
