Problem

Given a 1x1 square. Is it possible to put into it not intersecting circles so that the sum of their radii will be 1996?

Solution

It's an interesting problem. The number 1996 looks pretty much random and irrelevant. Chances are that either the problem in solvable for 1996 or it is solvable for other and larger numbers as well. Let us experiment. Start with simple configurations. If there is just one circle, how big its radius could be? 1/2. If my purpose at this point is to gain an insight into the problem, what simple configurations can I use? 2 circles? The result will be a half of the square's diagonal - .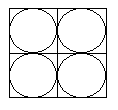

So I'll skip the case of three circles. Take four. Here's one possible configuration. The sum of radii is 1. In three experiments we obtained an increasing sequence of numbers: 1/2, , and 1. It may pay to continue with our experiment using simple configurations. Looking at the two pictures, it was easy to find the radius of a circle when it was inscribed into a square. First, it was the original 1x1 square. The last time, we had 4 smaller squares of the size 1/2x1/2 each. Dividing the square into nine 1/3x1/3 squares we'll get the sum of radii 1/6*9 = 3/2 - a new increase. With 16 squares the sum will be 1/8*16=2. With n² small squares, the sum will become 1/(2n)*n²=n/2.

Since n can be chosen arbitrary large there is no limit to the sum of radii of the circles packed into a 1x1 square.

Follow up

Let us replace the square with other shapes. Say, consider a circle of radius 1. Is it possible to put into a circle of radius 1 a number of not intersecting circles so that the sum of their radii will be 1996? Sounds amazing, right. My first attempt was to divide the circle into rings - something similar to dividing the square into narrow rectangles. But this compromised expected simplicity of the solution.

Still I was sure that the problems are somehow related and it should be possible to apply one when solving another. The solution is even more immediate than I first thought. First inscribe a square into the circle. Then solve the previous problem for the square thus obtained.

With this it becomes clear that the problem can be meaningfully formulated for various container shapes and for different small ones that should pack the given container.

Copyright © 1996-2008 Alexander Bogomolny