Solve - an Olympiad Problem - in Your Mind

The following problem has been offered at the 2006 Singapore Secondary Schools Mathematical Olympiad for Junior Section [Lecture Notes, p 3]:

On my attempt to solve the problem I have copied it this way:

\(\displaystyle \frac{1}{x^{2}-10x-29}+\frac{1}{x^{2}-10x-45}-\frac{1}{x^{2}-10x-69}=0. \)

Having figured out a solution I was surprised to discover that my equation had four roots - instead of two. However, the answers were not unrelated. I soon discovered my error and realized where the relation between the two answers came from. Both equations belong to a certain kind; the kind that allows one to see the sum of its roots practically at a glance.

Solution

References

1. Xu Jiagu, Lecture Notes on Mathematical Olympiad Courses, v 8, (For senior section, v 1), World Scientific, 2012

|Contact| |Front page| |Contents| |Up| |Algebra|

Copyright © 1996-2018 Alexander Bogomolny

It is hard to miss the fact that the three denominators all contain \(x^{2}-10x\). After completing the square, introduce a new variable:

\(y=(x-5)^2.\)

In terms of the so defined \(y\) the equation becomes:

\(\displaystyle \frac{1}{y-54}+\frac{1}{y-70}=\frac{2}{y-94} \)

which can be rewritten as

\( (2y-124)(y-94) = 2(y-54)(y-70), \)

or else

\( 2y^{2}-312y + 124\cdot 94 = 2y^2 - 248y + 2\cdot 54\cdot 70, \)

which is a linear equation \(64y = 4096\). From which \(y =64\). This leads to an equation in \(x\):

\( (x-5)^2 = 64, \)

so that, say, \(\alpha = 13\) and \(\beta =-3\), making \(\alpha+\beta=10\).

The same substitution in the mistyped case leads to a quadratic equation in \(y\), i.e., a quartic equation in \(x\). As a matter of fact, in order to find the sum of the roots of the polynomial equation of degree \(n,\) one only has to calculate the coefficient by \(x^{n-1}\) (Viète's theorem). But having to first solve an equation in \(y\), we then split the problem into solving several (1 or 2 or, in principle, more) quadratic equations, the sum of whose roots in the two cases at hand is \(10\). Thus the answer in my (mistyped) case was "the sum of the four roots is 20".

Below are two graphs (of the left-hand sides), one with two roots, the other with four:

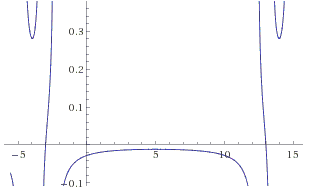
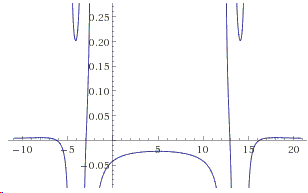
Where have the numbers \(10\) and \(20\) come from? Clearly, the source is the \(10\) in the common part of the denominators \(x^2-10x \ldots\) And next comes the insight:

The sum of all roots of an equation \(f(x)=0\), where \(f\) is an even function, is \(0\).

Now we adapt that to the equation at hand:

The sum of all roots of an equation \(f(x-a)=0\), where \(f\) is an even function, is a multiple of \(2a\). More accurately, the sum of the roots is equal to \(\displaystyle 2a\cdot\frac{n}{2}\), where \(n\) is the number (necessarily even) of roots.

With this in mind, you can modify the free terms in the denominators or the numerators and still get \(10\) or \(20\) as the sum of all roots; the answer being dependent on the number of roots or, in other words, on whether the simplified equation comes out linear or quadratic. This can be determined at a glance. Say, the sum of the roots of the equation below is \(-8\), even if some of the roots may be complex.

\(\displaystyle \frac{2}{x^{2}+8x-29}+\frac{5}{x^{2}+8x-45}-\frac{7}{x^{2}+8x-69}=0. \)

In a more general case, you do not even need to solve an equation in \(y\), but only ascertain its degree - the equation in \(x\) will have twice as many roots.

|Contact| |Front page| |Contents| |Up| |Algebra|

Copyright © 1996-2018 Alexander Bogomolny