The applet below simulates random selection of one or two clock hands. The dial face is split into red and pink regions whose number depends on the Sector settings and whose relative size is determined by the Ratio. The event of interest is a hand hitting red.
Obviously, when two hands are selected independently of each other, their probabilities of hitting red must be equal. But what happens if only the first hand is selected randomly while the second hand is drawn at a fixed Angle to the first one? How will such an arrangement affect the probabilities for the second hand? (When the Angle is zero, only one hand is thrown. Otherwise, there are two of them at the selected Angle.)
The string in the low right corner shows the number of red hits for the first (1) and the second (2) hand and the total number of Trials.
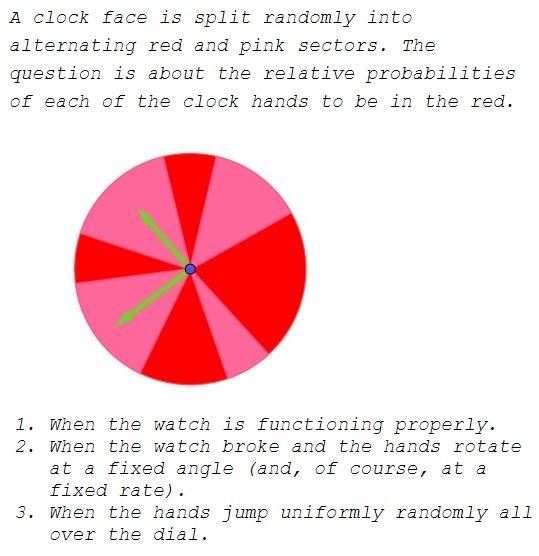
Discussion
As hard as it may be to believe, the probability of the second hand hitting red is independent of the fact that the two hands is rigidly attached at a certain angle. Imagine throwing the first hand randomly, attaching the second hand at a certain angle, but only drawing the latter. Would you think that the second hand (which actually appears alone) is less random or has a different probability of hitting red than the lone first hand?
To add a little more rigor to the above argument, let R be the set of red points on the unit circle. (Selecting a hand is equivalent to picking a point on the unit circle.) We may also think of it as a set Ro in the interval [0, 2p). Let A be the angle between the two hands. Selecting the second hand is equivalent to selecting a point in [0, 2p) and then shifting it by A, i.e. selecting a random point in [0, 2p) + A, or which is the same [A, 2p + A). The set Ro undergoes a shift into Ro + A, which has the same relative size as the set Ro. Furthermore, the original set R is clearly left unchanged by the shift. What does change is the point at which the circle is cut before being unfolded into a segment.
|Contact|
|Front page|
|Contents|
|Probability|
|Store|
|Activities|
Copyright © 1996-2012 Alexander Bogomolny
