Watt's and Chebyshev's Linkage
A parallel linkage is a device that consists of three straight segments AB, BD, CE, hinged at B and D and being able to rotate at the two fixed end points, A and E. It's probably hard to imagine a simpler device or the usefulness of this one.
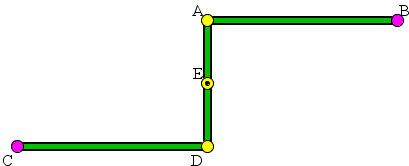
Yet it is said that the invention of the device by James Watt (1736 - 1819) around 1874 engendered the Industrial Revolution in England and the rest of the world. Mistakenly, Watt is often credited with the invention of the steam engine. What is true is that Watt's improvements made the steam engine so efficient as to make it useful in a variety of applications, locomotion being just one example.
The linkage wearing nowadays Watt's name transforms circular into a pretty much linear motion and vice versa. The inaccuracy did not prevent Watt's invention from becoming a driving force in the exploitation of steam engines. (Not long ago, the device has been used in car suspension by the Ford company.)
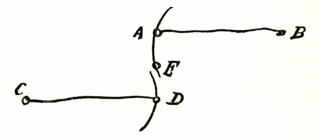
As could be seen above the midpoint E of the middle segment AD traces an 8-figure with two almost straight segments around the waist of the digit 8. The drawing below show the way Watt has gained insight for his invention. He explained this in a letter to his partner Matthew Boulton: "The convexities of the arches, lying in contrary directions, there is a certain point in the connecting-lever, which has very little sensible variation from a straight line."
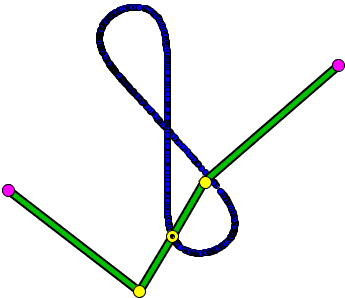
Notwithstanding the huge industrial progress due to Watt's invention, is was fitting for engineers and especially mathematicians to continue looking for better - more accurate - means of tracing a straight line. Half a century after Watt, the great Russian mathematician Pafnuty Chebyshev came up with another 3-rod linkage where pieces had differed in lengths from those of Watt's and two have been crossed.
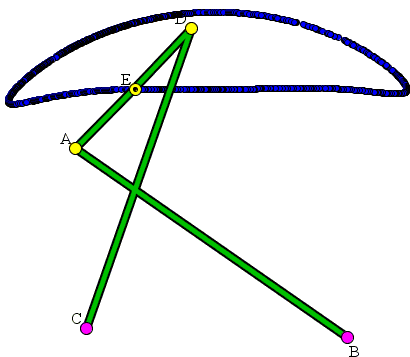
The device traces altogether a different curve having still a piece that looks almost straight. Chebyshev did not make any significant progress developing linkages but along the way has discovered the polynomials that now bear his name. A student of his, Yom Tov Lipkin, came up with a perfect mechanism that is presently known as Peaucellier's or sometimes Peaucellier-Lipkin Linkage. (In passing, "yom tov" is the Hebrew expression for "good day" or "holiday".)
The cover designer for a 1877 book How to Draw a Straight Line has clearly had in mind the curve drawn by Chebyshev's linkage:
The book starts with a discussion on the fine distinction between the two geometric tools used in Euclidean constructions: straightedge and compass. While the curve drawn by a compass is a circle according to Euclid's definition. Compass draws a circle from a scratch - so to speak. However, in order to be sure that following a straightedge with a pencil leads to a straight line, we have to be sure that the maker of the straightedge knew a priori how to draw a straight line. This question provides an extra (besides all the industrial applications) impetus for the investigation of the ways of converting between circular and linear motion.
The applet below is an interactive illustration for Watt's and Chebyshev's linkages. When the "Trace" button is checked, point E leaves a traces when either A or D are dragged. Note that occasionally, when, say, you drag A, D become almost collinear with C and E so that, at this point, A should be dragged back. Instead, switch to dragging the other point D. Similarly, when dragging D, if A becomes (almost) collinear with B and E and D gets blocked, switch to dragging A.
You can change the initial positions of the points and the rod lengths when the "Set points" button is checked.
(See that you do not always get the curves discovered by Watt and Chebyshev. It does take some insight to come up with a proper configuration.)
| What if applet does not run? |
References
- A. B. Kempe, How to Draw a Dtraight Line: A Lecture on Linkages, MacMillan & Co., 1877
- J. O'Rourke, How To Fold It: The Mathematics of Linkages, Origami and Polyhedra, Cambridge University Press, 2011
Linkages
- What Is Linkage?
- Peaucellier Linkage
- Hart's Inversor
- The Fundamental Theorem of 3-Bar Motion
- Pantograph
- Watt's and Chebyshev's Linkage
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73573917
