Vecten-Nikolin Hexagon

Vecten's configuration has been researched for a century and a half. It was shown to posses many engaging properties. But apparently the quest is not over yet. In May 2012 Vladimir Nikolin, an elementary school teacher from Serbia, has reported new discoveries. Three of these are illustrated by the applet below. What are they?

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at https://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

What if applet does not run?

Explanation

Vecten's configuration consists of three squares \(ABC_{b}C{a}\), \(BCA_{c}A_{b}\), and \(CAB_{a}B_{c}\) formed on the sides of an arbitrary \(\Delta ABC\). Lines \(AA_{c}\), \(AA_{b}\), cut side \(BC\) in points \(X_{c}\), \(Y_{b}\); lines \(BB_{a}\), \(BB_{c}\) cut side AC in points \(X_{a}\), \(Y_{c}\); lines \(CC_{b}\), \(CC_{a}\) cut side AB in \(X_{b}\) and \(Y_{a}\), respectively.

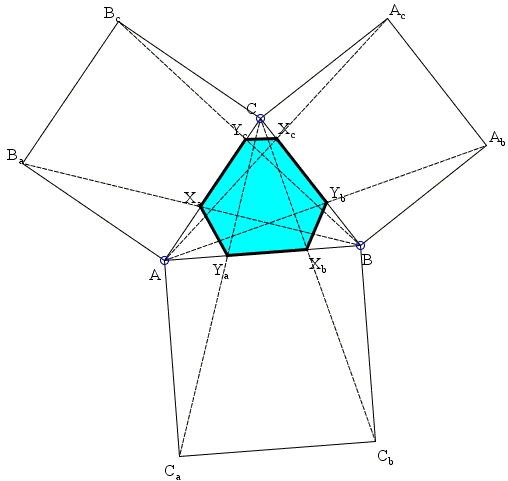
Vecten-Nikolin hexagon

The hexagon \(X_{a}Y_{a}X_{b}Y_{b}X_{c}Y_{c}\) has the following properties

\(X_{a}Y_{a}\)||\(X_{b}Y_{c}\), ...

Triangles \(X_{a}X_{b}X_{c}\) and \(Y_{a}Y_{b}Y_{c}\) have equal areas.

If \(N_{a}\) is the midpoint of \(X_{a}Y_{a}\), etc.; \(M_{a}\) the midpoint of BC, etc.; \(L_{a}\) the midpoint of \(X_{c}Y_{b}\), etc., then

\(N_{a}M_{a}\), \(N_{b}M_{b}\), \(N_{c}M_{c}\) are concurrent,
\(N_{a}L_{a}\), \(N_{b}L_{b}\), \(N_{c}L_{c}\) are concurrent.

As Vladimir showed and as the applet illustrates, all the above properties hold when the squares are replaced with similar rectangles.

... to be continued ...

72104047