Three Tangent Circles

Three circles (O_i), with centers at O_i, i = 1, 2, 3, touch pairwise externally. If i, j, k are three different indices obtained from 1, 2, 3 by a cyclic permutation, then P_k denotes the point of contact of (O_i) and (O_j). P_iP_j extended crosses again (O_i) in Q_k and (O_j) in R_k. Let r_i denote the radius of circle (O_i).

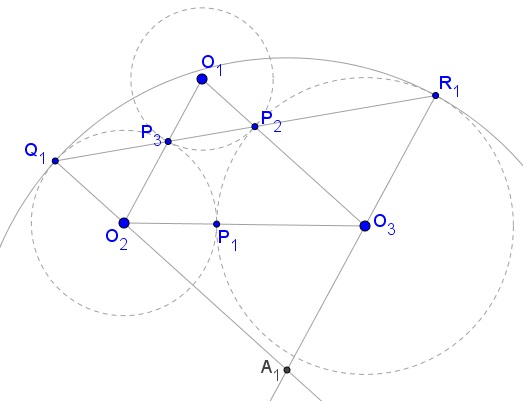
The center A_k of circle (A_k) lies at the intersection of lines C_iQ_k and C_jR_k. One passes through P_j, the other through P_i. Note that, say P_j, is the center of similarity of (O_i) and (O_k). Therefore, triangles P_jO_kP_i and P_jO_iQ_k are similar. Which makes lines O_kP_i and O_iQ_k parallel. Thus, O_kO_j||O_iA_k. Similarly, O_kO_i||O_jA_k. The quadrilateral O_iO_kO_jA_k is a parallelogram. Which implies

But the radius of circle (A_k) equals

Which means that the radius of circle (A_k) is the sum of the radii of the given three circles. Since there is nothing special about the index k, all three circles A have the same radius and are, therefore, equal.

References