Homologous Lines under Three Spiral Similarities
The following result is classic in the theory of three directly similar figures, see [Casey, Johnson, Lachlan, Yaglom].
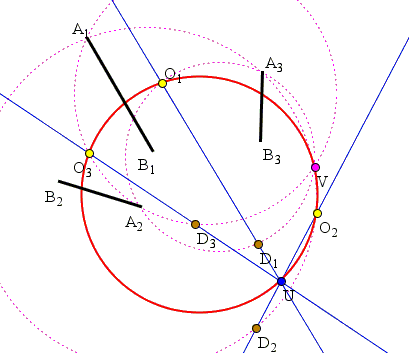
Let F1, F2, F3 be any three figures which are directly similar; let O1 be the center of similitude of F2 and F3; O2 that of F3 and F1; and O3 that of Fl and F2. The triangle formed by the three centers of similitude O1, O2, O3 is called the triangle of similitude of the figures F1, F2, F3; and the circumcircle of this triangle is called the circle of similitude. There is a good reason for this designation.
Theorem
| In every system of three directly similar figures, the triangle formed by three homologous lines is in perspective with the triangle of similitude, and the locus of the center of perspective is the circle of similitude. |
Two directly similar figures can always be obtained from each other by either rotation, homothety, translation, or, more generally, spiral similarity. The latter is a combination of rotation and homothety with the same center. It is just characterized by an angle (of rotation) and by a real number (the coefficient of homothety.)
Since the theorem deals with homologous (corresponding) line segments, in the applet below three similar figures are represented by the three segments A1B1, A2B2, A3B3. The center of the spiral similarity that maps A2B2 on A3B3 is O1, while O2 and O3 are the centers of transforms that map A3B3 on A1B1 and A1B1 on A2B2, respectively.
In the applet, the three segments can be dragged by their endpoints, causing a rotation around their other end or stretching their lengths, or by their midpoint, causing a translation. Checking the "construction" box shows the three pairs of circles that spiral similarity intersect at the centers of the three spiral similarities.
| What if applet does not run? |
References
- J. Casey, A Sequel to the First Six Books of the Elements of Euclid, University of Michigan, 2005 (reprint of 1888 edition), pp. 189-193
- R. A. Johnson, Advanced Euclidean Geometry , Dover, 2007 (reprint of 1929 edition), pp. 302-312
- R. Lachlan, An Elementary Treatise on Modern Pure Geometry, Cornell University Library (reprint of 1893 edition), pp. 140-142
- I. M. Yaglom, Geometric Transformations II, MAA, 1962, p. 82, pp. 163-165
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander BogomolnyProof
We shall prove a little more than stated in the theorem.
First of all, note that we are in a position to apply the Pivot Theorem which tells us that the circles D1A2A3, A1A2D3 and A1D2A3 intersect in a point (Hint A). Call it V. By the same token, circles D1B2B3, B1B2D3 and B1D2B3 also intersect in a point (Hint B). Call it W.
| What if applet does not run? |
Observe that by the construction of centers of similarity circles D1A2A3 and O1A2A3 coincide as are the circles A1A2D3, A1A2O3 and A1D2A3, A1O2A3. A similar assertion holds for the points B as well.
Let U be the intersection of lines D2O2 and D3O3. We'll show that the four points U, V, O2, O3 are concyclic. Since proving that U, V, O1, O3 are also concyclic is similar, it will then follow that the points O1 and O2 lie on the circle UVO3 so that all five of them -
U, V, O1, O2, O3 - are concyclic. Since V and W enter the problem in a symmetric fashion, W lies on the same circle. Furthermore, the same argument would have led to the same conclusion had we taken U to be the intersection
So, now everything hinges on proving that
|
we see that
| (1) | ∠O2VO3 + ∠D2O2V + ∠D3O3V + ∠O2UO3 = 360°. |
Since points D2, O2, V, A1 are concyclic,
| ∠D2O2V = 180° - ∠D2A1V. |
Since points D3, O3, V, A1 are concyclic,
| ∠D3O3V = ∠D3A1V. |
Taking into account that ∠D2A1V = ∠D3A1V,
| ∠O2VO3 + ∠O2UO3 = 180°, |
implying that points U, O2, V, O3 are concyclic, as required.
Note that the derivation relied heavily on the specifics of the point layout depicted in the diagram. For example, (1) was true because quadrilateral O2VO3U was convex. It need not be so. Had we set to prove that points U, O1, V, O3 were concyclic, we would have to proceed differently since, in the same diagram, quadrilateral O1VO3U is not convex (not even simple.) The ambiguity as well as the reliance on the diagram may have been avoided had we used directed angles modulo 180°.
(There are additional points on the circle of similitude. For example, if there are two triplets of homologous lines, their triangles D1D2D3 are directly similar with the center of the spiral similarity that maps one on the other lying on the circle of similitude, naturally.)
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73575261
