A Quadrilateral with 3 Equal Sides
What is this about?
A Mathematical Droodle

---

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at https://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

---

What if applet does not run?

Explanation

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

The applet lets you manipulate a quadrilateral, ABCD, so as to maintain the equality of three sides:

BC = CD = AD.

Let E be the point of intersection of the diagonals. An interesting situation occurs when also AE = BE. There are plenty of isosceles trapezoids each of which satisfies both conditions. However, there are quadrilaterals, other than trapezoids that also have these properties:

Following M. Hajja (The Mathematical Gazette, v. 94, n. 531, Nov. 2010), let's introduce angles α, β, ... as shown:

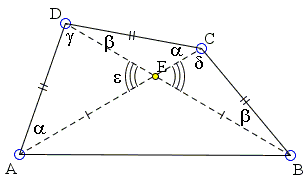
The focus of our interest are triangles ADE and BCE. In these triangles,

AE = BE, AD = BC, ∠AED = ∠BEC.

We are in a position to exploit the SSA situation. There are just two possibilities: Either the two triangles ADE and BCE are congruent, or γ + δ = 180°. The first case is impossible due to the third condition CE ≠ DE. If so, γ + δ = 180° is bound to hold. Summing up the angles in triangles ACD and BCD we get

2α + β + γ = 180°,
α + 2β + δ = 180°.

Adding the two and taking into account that γ + δ = 180° we obtain 3(α + β) = 180°, or

α + β = 60°.

But, by the Exterior Angle Theorem, ε = α + β, and we are done.

Furthermore, again by the Exterior Angle Theorem, ∠ABE + ∠BAE = 60°, implying ∠ABC + ∠BAD = 120°. But this means that the sides BC and AD meet at a 60° angle, which make the quadrilateral ABCD equilic.

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny