Areas and Centroid in a Triangle: What Is It About?
|
| Buy this applet What if applet does not run? |
|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|
Copyright © 1996-2012 Alexander Bogomolny
Areas and Centroid in a Triangle
The applet may suggest the following statement:
| From a point O inside ΔABC draw the lines OL, OM, ON parallel to the sides BC, AC, and AB, respectively so that, L lies on AB, M, on BC, and N on AC. It so happens that the areas of triangles BOL, COM, AON are equal. Prove that O is the centroid of ΔABC. |
| Buy this applet What if applet does not run? |
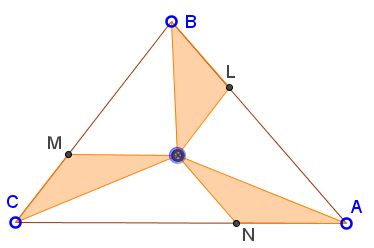
Proof
(For the proof, drag the inner point to coincide with the "target" point inside the triangle and press the "Hint" button.)
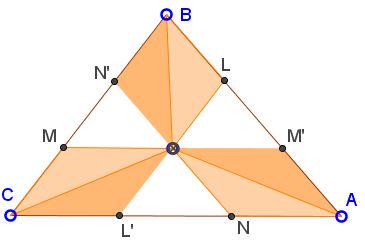
Let OL intersect AC in L'. Then
| Area(BOL) = Area(COM) = Area(COL'), |
such that
| Area(BOL) = Area(COL'). |
But since LL'||BC, the altitudes in triangles BOL and COL' (from B and C, respectively) are equal. Therefore,
| OL = OL', |
which implies that O lies on the median from vertex A. Similarly, it lies on the medians from B and C. Thus O is none other than the centroid of ΔABC.
Michel Cabart suggest an algebraic treatment to the problem based on the barycetric coordinates and their realization with with material points.
Let the barycentric coordinates of O be a, b, c with a + b + c = 1. O is thus the center of gravity of the three material points
| Area( ΔBOL) = 1/2 det(a·BA, c·BC) = ac·S, |
where S is area of ABC. The condition imposed is thus equivalent to
References
|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|
Copyright © 1996-2012 Alexander Bogomolny
| 40612237 |
