120° Breeds 90°
What Is This About?
A Mathematical Droodle
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander BogomolnyExplanation
The applet attempts to suggest a simple result from C. Bradley's article, The Fermat Point Configuration, in the Math Gazette (2008, pp. 214-222.)
Assume in $\Delta PQR,$ $\angle QPR = 120^{\circ};$ $H,$ $O,$ $I,$ N are the orthocenter, circumcenter, incenter, and the center of the 9-point circle, respectively. Then $PN \perp OH$ while $PI\parallel OH.$
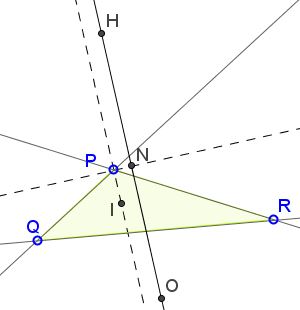
In case $\angle QPR = 60^{\circ},$ $PN \perp OH$ still holds while $I$ lies on $PN.$
$OH$ is the Euler line of $\Delta PQR$ and, as such, contains $N$ midway between $O$ and $H.$ Thus, $PN \perp OH$ is equivalent to $\Delta PHO$ being isosceles, in particular $PO = PH.$ However, $PO = R,$ the circumradius of $\Delta PQR.$ Also, $PH = 2R\cdot |\cos(\angle QPR)| = R$ implying that $PO = PH,$ as needed.
Concerning $PI,$ we know that the lines $PH$ and $PO$ are isogonal images of each other because $PI$ bisects one of the angles they form. This makes $PI$ either parallel or perpendicular to another bisector of one of the angles formed by $PH$ and $PO.$ When $\angle QPR = 120^{\circ},$ $PI$ and $PN$ are distinct and $PI \perp PN.$ When $\angle QPR = 60^{\circ},$ $PI$ and $PN$ coincide.
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73575976
