The MathPro Logo: What is this about?
A Mathematical Droodle
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
Explanation
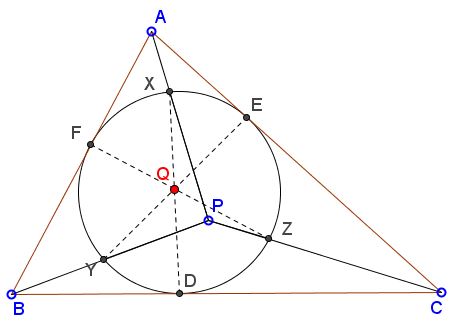
The applet is supposed to suggest the following fact. Let P be a point in the plane of ΔABC. Let D, E, F be the points of tangency of the incircle of ΔABC with the sides BC, AC, and AB, respectively. Join P to the vertices of the triangle and consider the points of intersection of the incircle by these lines. Denote the points X (on AP), Y (on BP), Z (on CP). Then the lines DX, EY, and FZ are concurrent.
The problem has been suggested by Stanley Rabinowitz as #1364 in the Mathematics Magazine (1990). He uses one of the configurations as the logo for his MathPro Press site and company. The company is a publisher and a distributor of fine math problem collections. Stanley himself is a regular contributor and problem solver for various math magazines.
The points of the concurrency illustrated by the applet is known as Rabinowitz's point. The point serves as a generalization of the Gergonne point.
Line AP crosses the incircle in two points as do lines BP and CP. The applet picks the points nearest the vertices. However if X', Y', Z' are the farthest from the vertices points, then, say DX, EY' and FZ' are also concurrent as are the triplets DX', EY and FZ' and DX', EY' and FZ.
Here is a proof by Nathan Bowler:
If P lies on the incircle, the result is trivial. So assume not.
Since the result deals only with tangency and concurrency, and there is a projective transformation fixing the incircle of ABC and taking P to the incentre, we may without loss of generality take P to be the incentre of ABC. But then by symmetry X lies at the midpoint of the arc EF so DX is the internal angle bisector of EDF. Similar statments hold for EY and FZ, so these three lines are concurrent at the incentre of DEF, as required.
Since DX', EY', FZ' are external bisectors of ΔEDF the triplets (DX, EY', FZ'), (DX', EY, FZ') and (DX', EY', FZ) are also concurrent, the triplet (DX', EY', FZ') is not.
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73582344
