Circles with Tangent Diameters

The applet below illustrates Problem 4 from the 1984 International Mathematics Olympiad:

Let ABCD be a convex quadrilateral such that the line CD is a tangent to the circle on AB as diameter. Prove that the line AB is a tangent to the circle on CD as diameter if and only if the lines BC and AD are parallel.

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at https://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

What if applet does not run?

Solution

Solution

Let O be the midpoint of AB and Q the midpoint of CD. The two circles at hand will be denoted (O) and (Q). We first show that if AB is tangent to (Q) and CD to (O), then AD||BC.

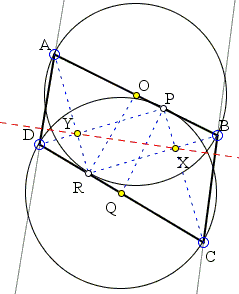
Let P be the point of tangency of AB and (Q) and R the point of tangency of CD and (O). Join P to C, D, and Q, and R to A, B, and O. By the assumption, OR ⊥CD and QP ⊥AB and also triangles ABR and CDP are right as formed on the diameters of (O) and (Q), respectively. It follows that OR is the median of ΔABR and QP is the median of ΔCDP, giving us several isosceles triangles: AOR (AO = OR), BOR (BO = OR), DPQ (DQ = PQ), CPQ (CP = PQ).

By construction,

	∠OBR	= ∠ORB
		= ∠ARB - ∠ARO
		= π/2 - (π/2 - ∠ARD)
		= ∠ARD.

(This identity also follows from the observation that the inscribed ∠ABR is subtended by the arc AR to which CD is tangent at R.)

Similarly,

∠OAR = ∠BRC,
∠QDP = ∠CPB,
∠RCP = ∠APD.

On the other hand, we know that, for example, ∠OAR + ∠OBR = π/2 (since ∠ARB = π/2) and also ∠QDP + ∠QCP = π/2. Let X be the intersection of CP and BR. Checking the angles in the triangles BPX and CRX, we see that

	0	= (∠CPB + ∠OBR + ∠BXP) - (∠RCP + ∠BRC + ∠CXR)
		= (∠CPB + ∠OBR) - (∠RCP + ∠BRC)
		= (∠CPB + ∠OBR) - (∠RCP + ∠OAR)
		= (∠CPB + ∠OBR) - (π/2 - ∠QDP) - (π/2 - ∠OBR)
		= (∠CPB + ∠OBR) - (π/2 - ∠CPB) - (π/2 - ∠OBR),

implying that ∠CPB + ∠OBR = π/2. The leaves the angle in ΔBPX at X equal π/2. If Y is the intersection of DP and AR, the quadrilateral PXRY is a rectangle, with opposite sides equal:

PY = RX and PX = RY.

Additionally, triangles APY, DRY, BPX, CRX are similar.

which shows that the right triangles ADY and CBX are also similar, so that ∠DAY + ∠CBX = π/2. Adding to this ∠ABR + ∠BAR = π/2 we see that ∠ABC + ∠BAD = π which proves that the lines BC and AD are indeed parallel.

(As a by-product of the above proportions, X and Y lie on the radical axis of the two circles so that XY passes through the two points where the circles meet.)

In the opposite direction, assume that BC||AD, DC tangent to (O) at R and P is the foot of the perpendicular from Q onto AB. We wish to show that ∠CPD is right, for then P will lie on (Q) making AB tangent to that circle.

... to be continued ...

72203067